5 Central Tendensi (Mean, Median, Modus, Kuartil, Persentil)

Tendensi sentral adalah ukuran statistik yang menunjukkan satu nilai yang mewakili pusat dari sekumpulan data. Ukuran ini memberi gambaran tentang di mana sebagian besar nilai dalam data biasanya berada. Dengan kata lain, tendensi sentral membantu kita mengetahui nilai yang paling mewakili keseluruhan data.

Secara umum terdapat 5 Tendensi Sentral atau Central Tendency yaitu :

Mean
Median
Modus
Kuartil
Persentil

Kita akan menggunakan data dummy berikut untuk menghitungnya

Partisipan	Nilai Kepuasan
0	72
1	13
2	67
3	11
4	71
5	18
6	43
7	32
8	60
9	87
10	51
11	13
12	80
13	61
14	49
15	66
16	86
17	78
18	49
19	49

Untuk mempermudah Analisis kita akan mengurutkan terlebih dahulu bagian dari tabel nilai kepuasan:

Partisipan	Nilai Kepuasan
17	11
19	14
13	15
10	22
1	25
15	38
4	39
6	45
3	58
18	59
0	61
2	61
8	64
9	65
12	67
14	68
16	79
7	81
5	86
11	87

1. Mean

Mean atau rata-rata adalah jumlah dari semua nilai dalam kumpulan data dibagi dengan banyaknya nilai dalam kumpulan data tersebut.

$$n = 20$$

$$Mean (\bar{x}) = \frac{\sum x_i}{n}$$

$$Mean (\bar{x}) = \frac{(11+14+15+22+25+38+39+45+58+59+61+61+64+65+67+68+79+81+86+87)}{20}$$

$$Mean (\bar{x}) = \frac{1045}{20}$$

$$Mean (\bar{x}) = 52,25$$

R Code

# data
nilai_kepuasan <- c(11, 14, 15, 22, 25, 38, 39, 45, 58, 59, 61, 61, 64, 65, 67, 68, 79, 81, 86, 87)

mean_nilai <- mean(nilai_kepuasan)
print(paste("Mean dari data tersebut sebesar:", mean_nilai))

Output : “Mean dari data tersebut sebesar: 52.25”

2. Median

Median adalah nilai tengah dari kumpulan data yang telah diurutkan dari yang terkecil hingga terbesar.

Karena jumlah data (n = 20) adalah genap, median adalah rata-rata dari dua nilai tengah.

Posisi dua nilai tengah adalah data ke-($\frac{n}{2}$) dan data ke-($\frac{n}{2}+1$).
Posisi ke-($\frac{20}{2}$) = data ke-10
Posisi ke-($\frac{20}{2}+1$) = data ke-11
- Data ke-10($x_{10}$) adalah 59.
- Data ke-11($x_{11}$) adalah 61.

$$Median (\mu) = \frac{x_{10}}{x_{11}}$$

$$Median (\mu) = \frac{59+61}{2}$$

$$Median (\mu) = \frac{120}{2}$$

$$Median (\mu) = 60$$

R Code

median_nilai <- median(nilai_kepuasan)
print(paste("Median dari data tersebut sebesar:", median_nilai))

Output : “Median dari data tersebut sebesar: 60”

3. Modus

Modus adalah nilai yang paling sering muncul dalam kumpulan data.

Pada data kita jika dihitung frekuensinya maka :

Nilai Kepuasan	Frekuensi
11	1
14	1
15	1
22	1
25	1
38	1
39	1
45	1
58	1
59	1
61	2
64	1
65	1
67	1
68	1
79	1
81	1
86	1
87	1

Pada kasus ini nilai modus untuk data di atas adalah 61 dengan frekuensi sebanyak 2.

R Code

# Fungsi untuk menghitung modus
hitung_modus <- function(x) {
  ux <- unique(x)
  tab <- tabulate(match(x, ux))
  modus_nilai <- ux[tab == max(tab)]
  frekuensi <- max(tab)
  return(list(modus = modus_nilai, frekuensi = frekuensi))
}

modus_hasil <- hitung_modus(nilai_kepuasan)
print(paste("Modus dari data tersebut sebesar:", paste(modus_hasil$modus, collapse=", "), 
            "dengan frekuensi:", modus_hasil$frekuensi))

Output : “Modus dari data tersebut sebesar: 61 dengan frekuensi: 2”

4. Kuartil

Kuartil membagi data menjadi empat bagian yang sama. Kuartil terbagi menjadi 3 yaitu Kuartil Bawah (Q1), Kuartil Tengah (Q2) dan Kuartil Atas (Q3).

Kuartil Bawah (Q1)

Posisi $Q1 = \frac{1}{4}(n+1)$

Posisi $Q1 = \frac{1}{4}(20+1)= \frac{21}{4} = 5.25$

Ini berarti Q1 terletak di antara data ke-5 dan data ke-6.

Data ke-5 = 25

Data ke-6 = 38

Q1 = Data ke-5 + 0.25 * (Data ke-6 - Data ke-5)

Q1 = 25 + 0.25 * (38 - 25)

Q1 = 25 + 0.25 * (13)

Q1 = 25 + 3.25

Hasil : Q1 = 28.2

Kuartil Tengah (Q2)

Q2 = Median($\mu$)

Q2 = 60

Kuartil Atas (Q3)

Posisi $Q3 = \frac{3}{4}(n+1)$

Posisi $Q3 = \frac{4}{3}(20+1)= \frac{63}{4} =15.75$

Ini berarti Q3 terletak di antara data ke-15 dan data ke-16.

Data ke-15 = 67

Data ke-16 = 68

Q3 = Data ke-15 + 0.75 * (Data ke-16 - Data ke-15)

Q3 = 67 + 0.75 * (68 - 67)

Q3 = 67 + 0.75 * (1)

Q3 = 67 + 0.75

Hasil : Q3 = 67.75

Jadi, kuartilnya adalah:

Q1 = 28.25
Q2 (Median) = 59.5
Q3 = 67.75

R Code

kuartil_nilai <- quantile(nilai_kepuasan)
print(kuartil_nilai)

Output :

0% 25% 50% 75% 100%

11.00 34.75 60.00 67.25 87.00

# Untuk mendapatkan Q1, Q2 (Median), Q3 secara spesifik:
Q1 <- quantile(nilai_kepuasan, 0.25)
Q2 <- quantile(nilai_kepuasan, 0.50) 
Q3 <- quantile(nilai_kepuasan, 0.75)

print(paste("Q1 (Kuartil Bawah):", Q1))
print(paste("Q2 (Median):", Q2))
print(paste("Q3 (Kuartil Atas):", Q3))

Output: “Q1 (Kuartil Bawah): 34.75”

[1] “Q2 (Median): 60”

[1] “Q3 (Kuartil Atas): 67.25”

Ada perbedaan di bagian nilai Q1 bukan, hal ini terjadi karena R secara default menggunakan metode interpolasi yang sedikit berbeda (dikenal sebagai type=7 dalam fungsi quantile). Kita akan menyesuaikan hasilnya di bagian selanjutnya.

Jika ingin membuat visualisasi, kita dapat memanfaatkan boxplot dengan:

# Membuat Box Plot
boxplot(nilai_kepuasan,
        main = "Box Plot Nilai Kepuasan Pengguna",
        ylab = "Nilai Kepuasan",
        col = "skyblue",
        border = "blue",
        horizontal = TRUE) 

# Atau lebih simpel, kita bisa melihat nilai-nilai ini dari summary()
summary_stats <- summary(nilai_kepuasan)
print("Ringkasan Statistik")
print(summary_stats)

Output:

“Ringkasan Statistik”

Min. 1st Qu. Median Mean 3rd Qu. Max.

11.00 34.75 60.00 52.25 67.25 87.00

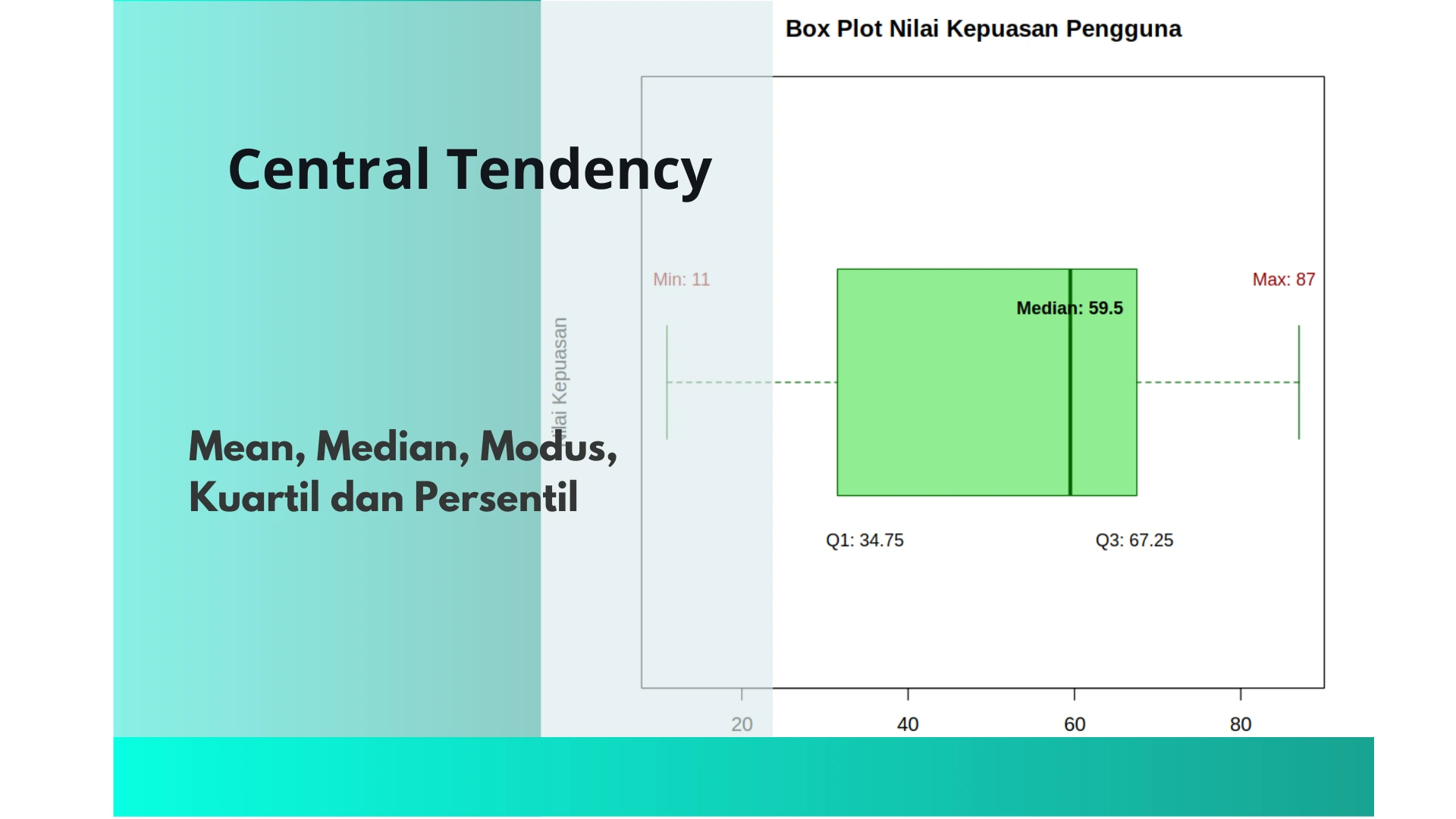
# Membuat Box Plot
boxplot(nilai_kepuasan,
        main = "Box Plot Nilai Kepuasan Pengguna",
        ylab = "Nilai Kepuasan",
                        col = "lightgreen", 
                        border = "darkgreen",
        horizontal = TRUE) 

# 2. Margin
par(mar = c(5, 4, 4, 2) + 0.1)

# Label untuk Min dan Max aktual
text(x = min_val+1.75, y = 1.15, labels = paste("Min:", min_val), pos = 3, col = "darkred", cex = 0.9)
text(x = max_val-1.75, y = 1.15, labels = paste("Max:", max_val), pos = 3, col = "darkred", cex = 0.9)

# Label untuk Q1, Median, Q3
text(x = q1_val, y = 0.75, labels = paste("Q1:", q1_val), pos = 1, col = "black", cex = 0.9)
text(x = median_val, y = 1.1, labels = paste("Median:", median_val), pos = 3, col = "black", font=2, cex = 0.9) 
text(x = q3_val, y = 0.75, labels = paste("Q3:", q3_val), pos = 1, col = "black", cex = 0.9)

5. Persentil

Persentil sebenarnya mirip dengan kuartil. Perbedaannya terletak pada jumlah pembagian data. Jika kuartil membagi data menjadi empat bagian yang sama besar, maka persentil membagi data menjadi seratus bagian yang sama besar. Artinya, setiap persentil menunjukkan posisi data dalam 1% interval dari distribusi.

Kuartil:

Q1 (25%)
Q2 (50%, median)
Q3 (75%)

Persentil:

Persentil ke-10 berarti 10% data berada di bawah nilai tersebut.
Persentil ke-90 berarti 90% data berada di bawah nilai tersebut.

Kita akan menghitung beberapa persentil umum, misalnya Persentil ke-10 (P10), Persentil ke-25 (P25), Persentil ke-50 (P50), Persentil ke-75 (P75), dan Persentil ke-90 (P90). Rumus umum untuk posisi persentil ke-k (Pk) adalah:

Posisi $Pk = \frac{k}{100}(n+1)$

Persentil ke-10 (P10)

Posisi $P10 = {10}{100}(20+1) = 0.10 \times 21 = 2.1$

Ini berarti P10 terletak di antara data ke-2 dan data ke-3.

Data ke-2 = 14
Data ke-3 = 15

P10 = Data ke-2 + 0.1 * (Data ke-3 - Data ke-2)

P10 = 14 + 0.1 * (15 - 14)

P10 = 14 + 0.1 * (1)

P10 = 14 + 0.1

Hasil : P10 = 14.1

Persentil ke-10 (P10) Dengan Metode R (type=7)

$$p = 0.10$$

$$h=(20 − 1) \times 0.10 + 1 = 19 \times 0.10 + 1 = 1.9 + 1 = 2.9$$

$$j=[h]=2 . \text{ Data ke-2 }(x_2) = 14, \text{ Data ke-3 }(x_3) = 15$$

$$P10 = x_2 + (2.9 − 2)(x_3 − x_2)$$

$$P10=14 + 0.9 \times (15−14)$$

$$P10=14 + 0.9 \times 1$$

$$P10=14.9$$

Akan sesuai dengan output R: “P10 (Persentil ke-10): 14.9”

Persentil ke-90 (P90)

Posisi $P90 = \frac{90}{100}(20+1) = 0.90 \times 21 = 18.9$ Ini berarti P90 terletak di antara data ke-18 dan data ke-19.

Data ke-18 = 81
Data ke-19 = 86

P90 = Data ke-18 + 0.9 * (Data ke-19 - Data ke-18)

P90 = 81 + 0.9 * (86 - 81)

P90 = 81 + 0.9 * (5)

P90 = 81 + 4.5

Hasil : P90 = 85.5

Persentil ke-90 (P90) Dengan Metode R (type=7)

$$p = 0.90$$

$$h=(20 − 1) \times 0.90 + 1 = 19 \times 0.90 + 1 = 17.1 + 1 = 18.1$$

$$j = [h] = 18 . \text{ Data ke-18 }(x_18) = 81, \text{ Data ke-19 }(x_19) = 86$$

$$P90 = x_18 + (18.1 − 18)(x_19 − x_18)$$

$$P90 = 81 + (0.1)(86 − 81)$$

$$P90= 81 + 0.1 \times 5$$

$$P90= 81 + 0.5$$

$$P90= 81.5$$

Akan Sesuai dengan output R: “P90 (Persentil ke-90): 81.5”

R Code

# Menghitung persentil ke-10 (P10)
P10 <- quantile(nilai_kepuasan, 0.10)
print(paste("P10 (Persentil ke-10):", P10))

# Menghitung persentil ke-90 (P90)
P90 <- quantile(nilai_kepuasan, 0.90)
print(paste("P90 (Persentil ke-90):", P90))

Output :

[1] “P10 (Persentil ke-10): 14.9”

[1] “P90 (Persentil ke-90): 81.5”

Reference :

Johnson, R. R., & Kuby, P. J. (2004). Elementary statistics (9th ed.). Brooks/Cole.

Partisipan	Nilai Kepuasan
0	72
1	13
2	67
3	11
4	71
5	18
6	43
7	32
8	60
9	87
10	51
11	13
12	80
13	61
14	49
15	66
16	86
17	78
18	49
19	49

Partisipan	Nilai Kepuasan
17	11
19	14
13	15
10	22
1	25
15	38
4	39
6	45
3	58
18	59
0	61
2	61
8	64
9	65
12	67
14	68
16	79
7	81
5	86
11	87

Partisipan	Nilai Kepuasan
0	72
1	13
2	67
3	11
4	71
5	18
6	43
7	32
8	60
9	87
10	51
11	13
12	80
13	61
14	49
15	66
16	86
17	78
18	49
19	49

Partisipan	Nilai Kepuasan
17	11
19	14
13	15
10	22
1	25
15	38
4	39
6	45
3	58
18	59
0	61
2	61
8	64
9	65
12	67
14	68
16	79
7	81
5	86
11	87

5 Central Tendensi (Mean, Median, Modus, Kuartil, Persentil)

1. Mean

R Code

2. Median

R Code

3. Modus

R Code

4. Kuartil

Kuartil Bawah (Q1)

Kuartil Tengah (Q2)

Kuartil Atas (Q3)

R Code

5. Persentil

Persentil ke-10 (P10)

Persentil ke-10 (P10) Dengan Metode R (type=7)

Persentil ke-90 (P90)

Persentil ke-90 (P90) Dengan Metode R (type=7)

R Code

Reference :

Related Posts

Partisipan	Nilai Kepuasan
0	72
1	13
2	67
3	11
4	71
5	18
6	43
7	32
8	60
9	87
10	51
11	13
12	80
13	61
14	49
15	66
16	86
17	78
18	49
19	49

Partisipan	Nilai Kepuasan
17	11
19	14
13	15
10	22
1	25
15	38
4	39
6	45
3	58
18	59
0	61
2	61
8	64
9	65
12	67
14	68
16	79
7	81
5	86
11	87