Melanjutkan pembahasan kita mengenai price optimization, seperti yang telah diulas dalam tulisan sebelumnya tentang Price Optimization: Menentukan Harga Optimal dari Kurva Permintaan, kali ini kita akan mencoba pendekatan yang lebih praktis dengan menggunakan Microsoft Excel. Berbeda dengan metode konseptual sebelumnya, di sini kita akan memanfaatkan sebuah add-ins atau fitur tambahan bawaan Excel yang sangat powerful untuk analisis optimisasi, yaitu Solver.
Solver merupakan sebuah add-ins pada Microsoft Excel yang dirancang khusus untuk melakukan analisis ‘what-if’ dan mencari solusi optimal terhadap suatu masalah. Secara teknis, Solver bekerja dengan cara menemukan nilai maksimum, minimum, atau nilai spesifik tertentu untuk sebuah formula dalam satu sel (disebut objective cell atau sel tujuan) dengan mengubah nilai-nilai dalam sel-sel lain (disebut variable cells atau sel variabel), sambil memastikan bahwa serangkaian batasan atau kondisi (disebut constraints) terpenuhi.
Dalam konteks optimisasi harga, Solver dapat membantu kita menentukan harga jual produk yang akan memaksimalkan keuntungan atau pendapatan, dengan mempertimbangkan fungsi permintaan dan batasan-batasan lain seperti biaya produksi atau kapasitas.
Optimisasi Harga Sederhana dengan Excel Solver: Memaksimalkan Profit
Dalam dunia bisnis, menentukan harga jual yang tepat adalah kunci untuk memaksimalkan keuntungan. Terkadang, kita hanya memiliki data penjualan historis terbatas. Bagaimana cara memanfaatkannya untuk menentukan harga yang lebih optimal? Di artikel ini, kita akan memandu Anda langkah demi langkah menggunakan fitur Solver di Microsoft Excel untuk melakukan optimisasi harga sederhana berdasarkan dua titik data historis.
Skenario: Misalkan kita memiliki data penjualan sebelumnya:
- Saat harga (Price) Rp 4.000, penjualan (Demand) adalah 20 unit.
- Saat harga Rp 4.500, penjualan turun menjadi 16 unit.
- Biaya per unit produk (COGS - Cost of Goods Sold) kita adalah Rp 2.000 (ini kita asumsikan atau dapatkan dari data biaya).
Mari kita siapkan data ini di Excel:
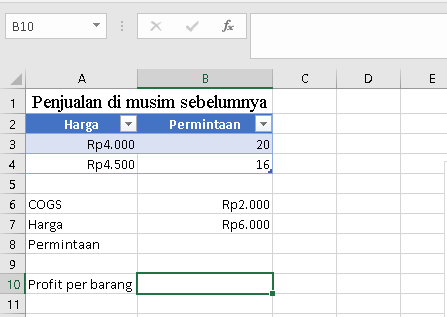
Langkah 1: Memodelkan Kurva Permintaan (Sederhana)
Untuk memprediksi bagaimana permintaan berubah seiring perubahan harga, kita perlu membuat model permintaan. Dengan hanya dua titik data, model paling sederhana adalah garis lurus (linear).
- Buat Scatter Plot: Blok data harga dan permintaan Anda (misal A3:B4 jika mengikuti gambar awal, atau siapkan data harga dan permintaan Anda). Pilih
Insert > Charts > Scatter.
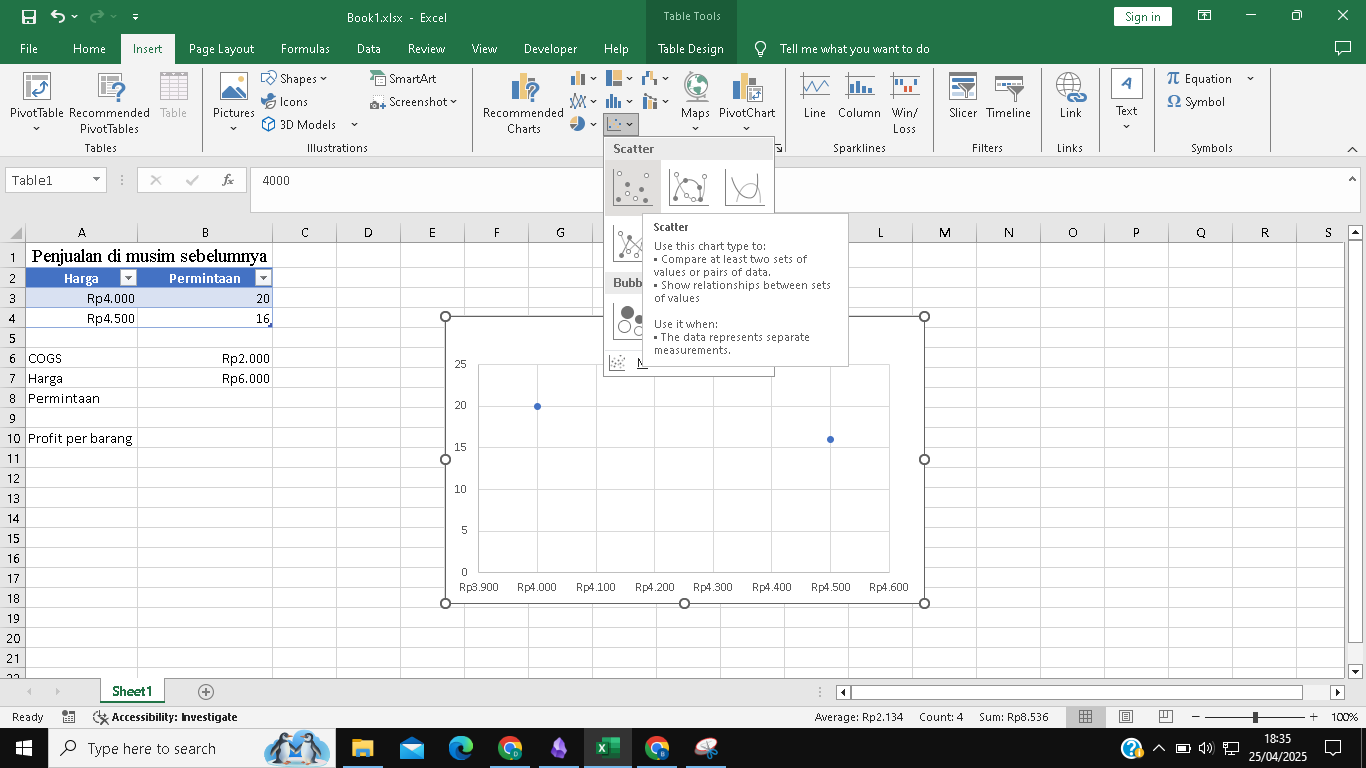
- Tambahkan Trendline: Klik kanan pada salah satu titik data di grafik, lalu pilih
Add Trendline.
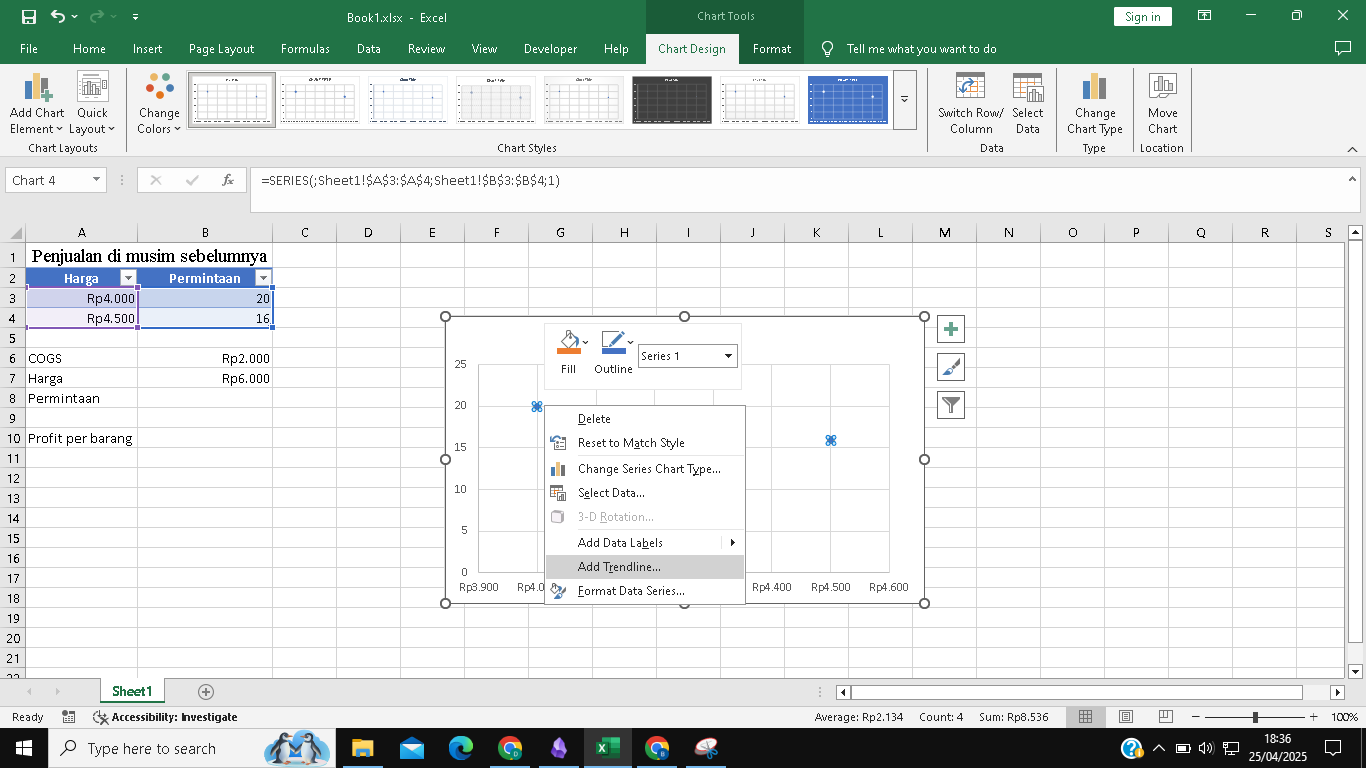
- Tampilkan Persamaan: Di panel
Format Trendlineyang muncul di sebelah kanan, gulir ke bawah dan centang kotakDisplay Equation on chart. Excel akan menampilkan persamaan garis yang paling sesuai dengan data Anda. Dalam contoh ini, persamaannya adalahy = -0.008x + 52.
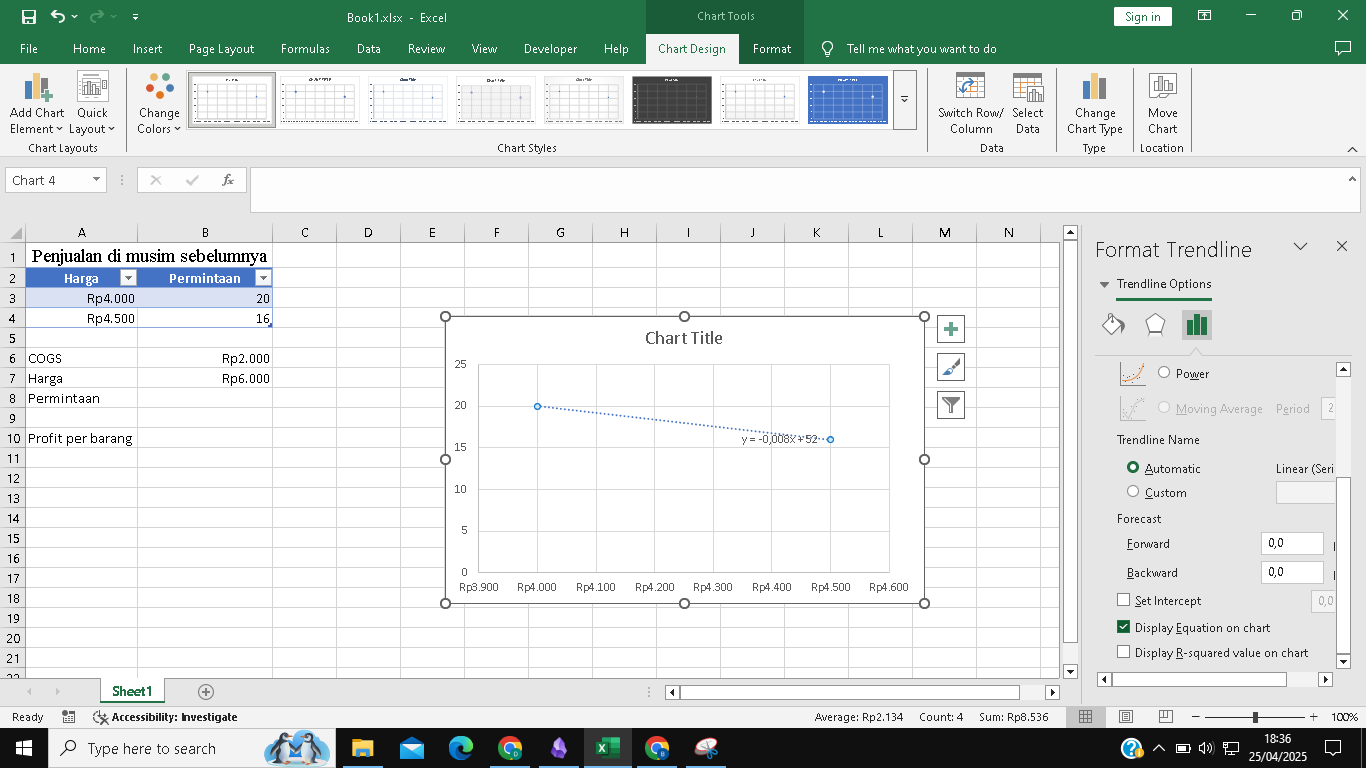
Persamaan y = -0.008x + 52 ini adalah model kurva permintaan linear kita. Artinya:
yadalah prediksi Permintaan (Demand).xadalah Harga (Price).- Formula ini menyatakan bahwa untuk setiap kenaikan harga sebesar Rp 1, permintaan diprediksi turun sebesar 0.008 unit. Angka 52 adalah titik potong teoritis jika harga nol (interpretasi ini perlu hati-hati dalam konteks nyata).
Penting: Model linear dari dua titik data adalah penyederhanaan besar. Di dunia nyata, kurva permintaan mungkin tidak linear dan Anda idealnya membutuhkan lebih banyak data. Namun, ini adalah titik awal yang baik untuk ilustrasi.
Langkah 2: Menyiapkan Perhitungan Profit di Excel
Sekarang, mari kita gunakan persamaan permintaan ini untuk menghitung potensi profit di Excel.
Siapkan Sel Input:
- Di sel
B6(misalnya), masukkan COGS Anda:2000. - Di sel
B7, kita akan memasukkan Harga jual. Awalnya, kita bisa coba masukkan salah satu harga historis, misal4000.
- Di sel
Hitung Prediksi Permintaan:
- Di sel
B8, masukkan formula berdasarkan persamaan trendline, denganB7sebagai input Harga (x):=-0.008 * B7 + 52Jika B7 adalah 4000, B8 akan menampilkan 20 (sesuai data awal kita). Jika Anda mencoba B7=6000, B8 akan menjadi 4.
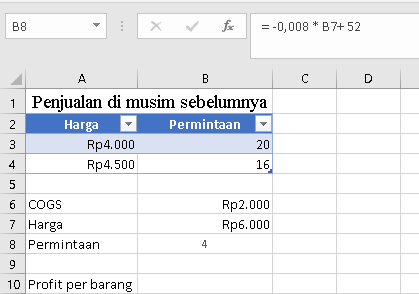
- Di sel
Hitung Profit:
- Profit dihitung sebagai:
(Harga Jual - COGS) * Prediksi Permintaan. - Di sel
B10, masukkan formula:=(B7 - B6) * B8Jika B7=4000, B6=2000, dan B8=20, maka B10 akan menjadi (4000-2000)*20 = 40.000. Jika B7=6000, B6=2000, dan B8=4, maka B10 akan menjadi (6000-2000)*4 = 16.000.

Tujuan kita adalah mencari nilai di
B7(Harga) yang membuat nilai diB10(Profit) menjadi maksimal.- Profit dihitung sebagai:
Langkah 3: Menggunakan Excel Solver untuk Optimisasi
Di sinilah Solver berperan. Solver akan mencoba berbagai nilai Harga (B7) secara otomatis untuk menemukan nilai yang memberikan Profit (B10) tertinggi.
- Buka Solver: Pergi ke tab
Datadan klikSolver(biasanya terletak di grup “Analyze” di paling kanan). Jika Anda tidak melihat Solver, Anda mungkin perlu mengaktifkannya melaluiFile > Options > Add-ins > Excel Add-ins > Go... > centang Solver Add-in.
Konfigurasi Solver:
- Set Objective: Pilih sel
B10(sel Profit kita). Pastikan opsiMax(Maximize) terpilih, karena kita ingin memaksimalkan profit. - By Changing Variable Cells: Pilih sel
B7(sel Harga yang ingin kita optimalkan). - Subject to the Constraints: (Ini langkah penting yang sering terlewat) Kita perlu menambahkan batasan agar hasilnya realistis:
- Klik
Add. MasukkanB8 >= 0(Prediksi Permintaan tidak boleh negatif). KlikAdd. - Masukkan
B7 >= B6(Harga Jual setidaknya harus sama dengan atau lebih besar dari COGS agar tidak rugi per unit). KlikOK.
- Klik
- Select a Solving Method: Pilih
GRG Nonlinear. Metode ini cocok untuk masalah dengan kurva (seperti model permintaan kita, meskipun linear, Solver akan menanganinya) dan fungsi tujuan yang mungkin tidak linear (profit adalah hasil kali harga dan permintaan).
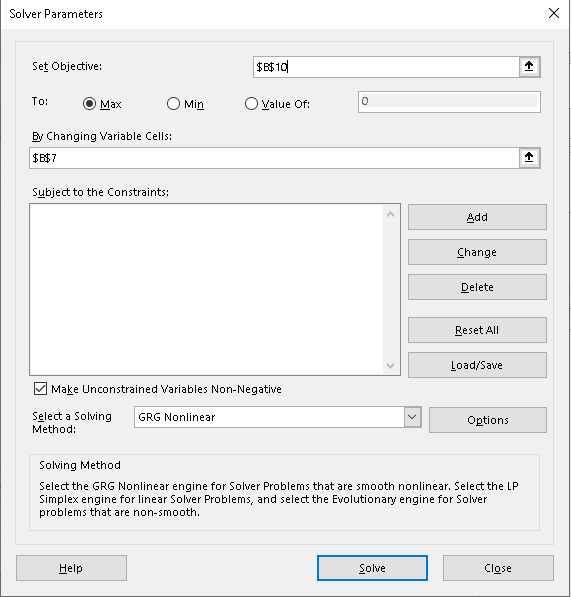
- Set Objective: Pilih sel
Jalankan Solver: Klik tombol
Solve.
Langkah 4: Hasil Optimisasi
Solver akan mencari solusi. Jika berhasil, akan muncul dialog “Solver Results”.
- Pilih “Keep Solver Solution” dan klik
OK.
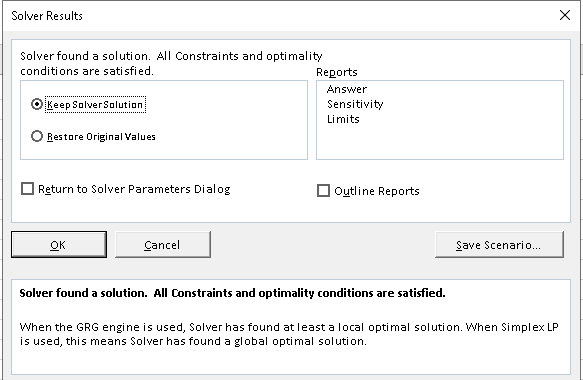
- Lihat Hasilnya: Perhatikan sel
B7(Harga) danB10(Profit). Solver telah mengubah nilai Harga ke angka yang (menurut model kita) akan menghasilkan Profit maksimal. Anda akan melihat nilai Profit (B10) sekarang lebih tinggi dibandingkan saat Anda menggunakan harga awal (misalnya Rp 4.000 atau Rp 6.000).
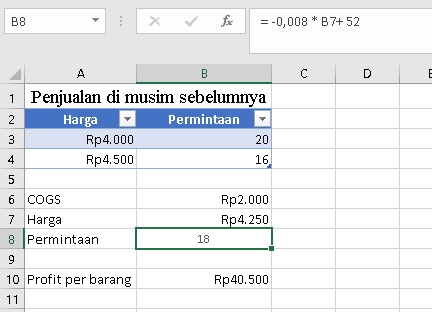
Dalam contoh ini, Solver menemukan bahwa harga optimal (berdasarkan model linear sederhana ini) adalah sekitar Rp 4.250, yang menghasilkan prediksi permintaan 18 unit dan profit maksimal Rp 40.500.
Video singkat
Price Optimization with Solver from Youtube.com
Kesimpulan
Excel Solver adalah alat yang ampuh untuk melakukan optimisasi harga, bahkan dengan data awal yang terbatas. Dengan memodelkan hubungan antara harga dan permintaan (meskipun secara sederhana) dan mendefinisikan tujuan (memaksimalkan profit), Solver dapat membantu Anda menemukan titik harga yang lebih baik daripada sekadar menebak atau menggunakan harga historis.
Ingat: Kualitas hasil optimisasi sangat bergantung pada kualitas model permintaan Anda. Semakin banyak data yang Anda miliki dan semakin akurat model Anda mencerminkan realitas pasar, semakin baik pula hasil optimisasi harga yang akan Anda dapatkan. Selamat mencoba!
