Dawn menekankan untuk memastikan keberlangsungan suatu bisnis, pengusaha setidaknya harus menetapkan harga jual produknya sebesar 45% di atas biaya produksi (Cost of Goods Sold atau COGS). Selain itu, tolak ukur minimal untuk gross margin yang disarankan adalah setara dengan atau lebih besar dari 30% dari nilai net revenue.

Sebagai contoh, jika biaya produksi (COGS) suatu produk adalah Rp. 100.000, maka harga jual yang direkomendasikan adalah minimal Rp. 145.000 (45% di atas COGS). Dengan harga jual tersebut, gross margin (pendapatan kotor)-nya adalah:

Dengan demikian, gross margin (pendapatan kotor) yang dihasilkan memenuhi tolak ukur minimal sebesar 30% dari net revenue, yang merupakan indikator sehat untuk keberlangsungan bisnis.

Selain, penting bagi kita untuk mengetahui nilai minimal dari penjualan kita. Ada faktor lain yang tidak kalah penting, yaitu menganalisis volume pembelian konsumen terkait harga yang ditetapkan. Faktor ini menjadi kunci dalam menilai sejauh mana perubahan harga memengaruhi minat beli pelanggan.

Konsep ini merujuk pada kurva permintaan (demand curve), yaitu grafik yang menggambarkan hubungan terbalik dari harga suatu produk/jasa dengan jumlah permintaan di pasar. Dengan mempelajari kurva ini, kita dapat mengidentifikasi titik optimal harga: saat kenaikan harga tidak menyebabkan penurunan drastis permintaan, atau sebaliknya, saat penurunan harga justru meningkatkan volume penjualan secara signifikan. Materi ini memungkinkan penyusunan strategi harga yang tidak hanya meningkatkan profitabilitas, tetapi juga mempertahankan daya saing produk kita di pasar.

Demand Curve

Elasticity

Sebelum masuk ke pembahasaan kurva permintaan, kita harus mengetahui terlebih dahulu terkait dengan konsep elastisitas. Elastisitas mengukur sejauh mana perubahan harga memengaruhi jumlah permintaan atau penawaran suatu produk. Dengan memahami elastisitas, kita dapat menilai apakah produk bersifat elastis—di mana perubahan harga secara signifikan memengaruhi permintaan—atau inelastis, di mana perubahan harga tidak banyak berpengaruh.

Misalnya ketika bisnis Anda menjual apple yang dijual seharga Rp. 12.000/ Kg, dengan penjualan sebanyak 300 Kg pada bulan sebelumnya. Karena Anda merasa cukup menguntungkan, Anda menaikkan harga sebesar Rp. 20.000/ Kg-nya di bulan ini. Saat Anda mencatat laporan ternyata penjualan turun drastis menjadi 150 Kg. Karena Anda penasaran Andapun menanyakan alasan kepada pelanggan setia Anda, dan ia mengungkapkan bahwa harga yang Anda tetapkan terlalu tinggi sehingga mengurangi niat mereka untuk membeli. Inilah yang disebut sebagai produk elastis.

Berbeda dengan permintaan elastis, permintaan inelastis terjadi ketika perubahan harga suatu produk atau jasa tidak signifikan memengaruhi jumlah permintaan konsumen. Dalam konteks ini, konsumen cenderung tetap membeli produk tersebut meskipun harganya naik. Fenomena ini sering ditemui pada produk atau layanan yang bersifat kebutuhan primer atau hidup-mati, seperti obat-obatan, bahan bakar, atau layanan kesehatan.

Contoh nyata dapat dilihat pada bisnis bahan bakar berkendaraan, seperti Pertalite. Bahan bakar jenis ini memiliki permintaan yang sangat inelastis karena menjadi kebutuhan dasar bagi masyarakat, baik untuk transportasi sehari-hari, pengiriman barang, maupun operasional industri. Meskipun harga bahan bakar ini naik, konsumen tetap harus membelinya karena merasa kesulitan mencari alternatif pengganti yang mudah diakses dan terjangkau.

Pengukuran

Di sini kita menggunakan data retail yang dapat kita unduh dari Kaggle.

Library yang Dibutuhkan

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import statsmodels.api as sm
from scipy.stats import t as t_dist
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

Library yang Dibutuhkan

df = pd.read_csv("retail_price.csv")
df.head()

Load Data

df = pd.read_csv("retail_price.csv")
df.head()

Ketersediaan Variabel

df = pd.read_csv("retail_price.csv")
df.head()

Mengambil Variabel yang dibutuhkan

df1 = df.copy()
df1 =  df1[df1["product_id"]=="bed1"]
df2 = df1[["product_id", "unit_price", "lag_price", "qty", "total_price", "month_year", "comp_1","ps1", "comp_2", "ps2", "comp_3", "ps3"]].head(30)
df2.head()

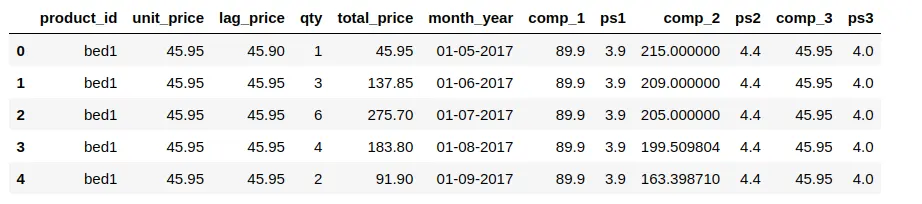
Di sini kita akan mencoba untuk menganalisa optimisasi harga untuk 1 produk yaitu bed1 serta kita juga mengambil variabel kompetitor (“com_”) sebagai perbandingan harga nantinya. Data kita terdiri dari kolom :

• product_id: Kode unik yang digunakan untuk mengidentifikasi suatu produk. Setiap produk memiliki ID yang berbeda-beda.
• unit_price: Harga per unit dari suatu produk. Ini adalah nilai jual yang ditetapkan untuk satu unit produk.
• lag_price: Harga produk pada periode sebelumnya (misalnya, bulan sebelumnya). Kolom ini digunakan untuk membandingkan perubahan harga dari waktu ke waktu.
• qty: Kuantitas atau jumlah unit produk yang terjual dalam periode tertentu.
• total_price: Total pendapatan yang dihasilkan dari penjualan produk, dihitung dengan mengalikan unit_price dengan qty.
• month_year: Periode waktu (bulan dan tahun) yang menunjukkan kapan data penjualan tersebut tercatat.
• comp_1, comp_2, comp_3: Harga produk dari kompetitor 1, 2, dan 3. Ini adalah harga yang ditawarkan oleh pesaing untuk produk sejenis.
• ps1, ps2, ps3: Persentase penjualan (market share) yang dimiliki oleh kompetitor 1, 2, dan 3. Kolom ini menunjukkan seberapa besar pangsa pasar yang dikuasai oleh masing-masing kompetitor.

Price Elasticity

df_elastic = df2.copy()
df_elastic = df_elastic[["product_id","qty","unit_price"]]
df_elastic.unit_price.value_counts()

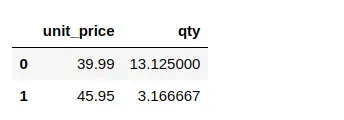
Seperti yang terlihat di atas jika jumlah unit_price lebih sering dilakukan pada harga 39.00 dan 45.95 sehingga kita dapat mengambil nilai rata-rata qty pada kedua unit_price tersebut

Melakukan Groupby untuk Mengambil Average Quantity dari Unit Price

df_elastic = df_elastic[df_elastic.duplicated(subset=['unit_price'], keep=False)]
df_elastic = df_elastic.groupby("unit_price")["qty"].mean().reset_index()
df_elastic

Mengukur Elastisitas

Untuk mengukur elastisitas kita dapat melakukannya dengan rumus :

# Hitung persentase perubahan kuantitas dan harga
df_elastic["%_change_qty"] = df_elastic["qty"].pct_change() * 100
df_elastic["%_change_price"] = df_elastic["unit_price"].pct_change() * 100

# Mengitung elastisitas
df_elastic["elasticity"] = df_elastic["%_change_qty"] / df_elastic["%_change_price"]
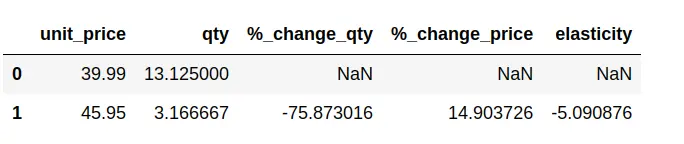
df_elastic

Seperti yang kita lihat nilai elastisitas dari produk ini sebesar -5.09 yang artinya bersifat elastis karena nilai absolut > 1. Tanda negatif menunjukkan hubungan terbalik antara harga dan kuantitas (harga turun maka kuantitas naik). Penurunan harga sebesar 1% menyebabkan kenaikan permintaan sebesar 5.09%.

Karna produk tersebut merupakan elastic product maka kita akan menghitung nilai dari demand curve untuk menghitung optimasi profit (profit optimization)

Profit Optimization

Menghitung Nilai Korelasi

df2[["unit_price","qty"]].corr()

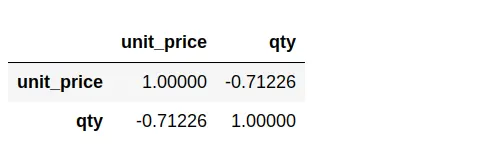
Seperti nilai elastisitas sebelumnya, nilai korelasi -0.71 menandakan adanya hubungan negatif antara Unit Price terhadap Quantity.

Nilai Slope dan Intercept

# Permintaan =  Harga(slope) + intercept
X = df2["unit_price"]
y = df2["qty"]
X = sm.add_constant(X)
# Jalankan regresi OLS
results = sm.OLS(y, X).fit()
print(results.summary())

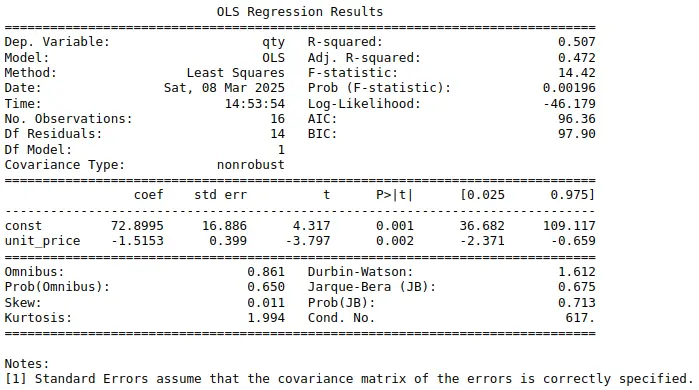
Pada nilai hipotesis tersebut nilai P>|t| yang menantakan nilai dari p-value bernilai 0.002 (p-value <0.05) pada variabel unit_price, yang menjelaskan adanya hubungan antara qty dengan unit_price.

intercept = round(results.params[0],2)
slope = round(results.params[1],2)

print(f"Permintaan = Harga({slope}) + {intercept}")

Mengukur Optimasi Harga

Karena pada data tidak diberitahu nilai dari COGS untuk produknya, kita perkirakan jika nilainya sebesar $30.

unit_cost = 30 # Estimasi COGS
increment_start=0.01
increment_end=25
step=0.05


# Ambil nilai intercept dan slope
intercept = results.params[0]
slope = results.params[1]

# Buat array harga dengan increment
increment = np.arange(increment_start, increment_end, step)
price = unit_cost + increment

# Hitung permintaan berdasarkan model
demand = (price * slope) + intercept
total_revenue = price * demand
profit = (price - unit_cost) * demand

# Buat DataFrame hasil
df_results = pd.DataFrame({
        "Price": price,
        "Demand": demand,
        "Unit Cost": unit_cost,
        "Total Revenue": total_revenue,
        "Profit": profit
    })
df_results

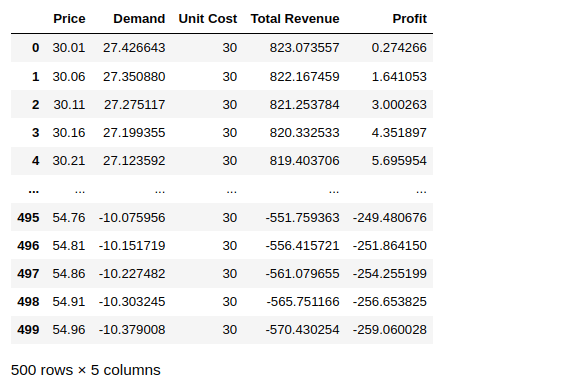
Pada tabel di atas, kita dapat melihat nilai dari setiap perubahan harga (Price) yang semakin tinggi menyebabkan permintaan (Demand) yang semakin rendah. Begitu juga perubahan harga berpengaruh terhadap total pendapatan (Total Revenue) serta keuntungan (Profit).

# Cari harga dengan profit maksimal
max_profit_idx = df_results["Profit"].idxmax()
optimal_demand = df_results.loc[max_profit_idx, "Demand"]
optimal_price = df_results.loc[max_profit_idx, "Price"]
max_profit = df_results.loc[max_profit_idx, "Profit"]

# Plot garis vertikal pada harga optimal
plt.axvline(x=optimal_price, color='r', linestyle='--', linewidth=1)

# Plot Line Chart
plt.plot(df_results["Price"], df_results["Profit"], linestyle='-')


# Tambahkan marker untuk profit maksimal
plt.scatter(optimal_price, max_profit, color='red', zorder=5)
plt.annotate(f'Max Profit: ${max_profit:.2f}\nwhen Price: ${optimal_price:.2f}\nand Demand {optimal_demand:.2f}',
             (optimal_price, max_profit),
             textcoords="offset points",
             xytext=(-80,30),
             ha='center',
             arrowprops=dict(arrowstyle="->"))

# Penyempurnaan tambahan
plt.title(f"Profit Optimization Curve")
plt.xlabel("Unit Price ($)")
plt.ylabel("Total Profit ($)")
plt.ylim(0, max_profit * 1.5)
plt.grid(False)
plt.legend()
plt.tight_layout()

# Tampilkan grafik
plt.show()

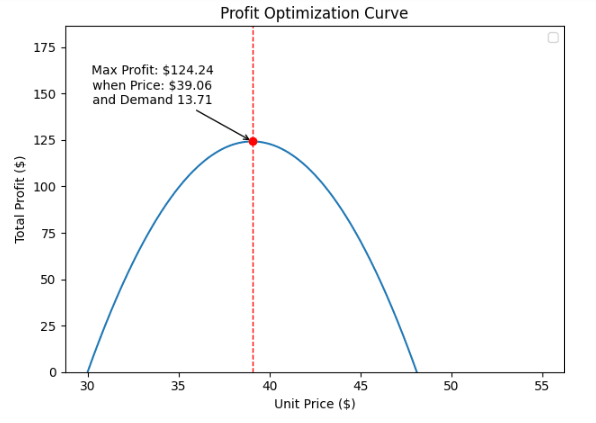
Merujuk pada kurva di atas, dapat dilihat jika maksimal keuntungan (Profit) yang dapat kita peroleh sebesar $124.24 dengan harga (Price) $39.06 dengan perkiraan permintaan (Demand) sebesar 13.17 produk. Dari data historis pembelian konsumen kita dapat memprediksi nilai harga untuk menghasilkan penghasilan maksimal.

Price Optimization Storytelling with Data

from matplotlib.font_manager import FontProperties
from drawarrow import ax_arrow
from highlight_text import fig_text, ax_text
import matplotlib.patches as patches

# Load font
bold_font = FontProperties(family="serif", weight="bold", size=10)

# Harga kompetitor bulan terakhir
df3 = df2.copy()
df3 = df3.tail(1)
low_price_comp = df3[[ "comp_1" , "comp_2", "comp_3" ]].T.min().reset_index().iloc[ 0, 1]
high_price_comp = df3[[ "comp_1" , "comp_2", "comp_3" ]].T.max().reset_index().iloc[ 0, 1]

#Nilai maksimal dari setiap Variabel
max_profit_idx = df_results["Profit"].idxmax()
optimal_price = df_results.loc[max_profit_idx, "Price"]
optimal_unit_cost = df_results.loc[max_profit_idx, "Unit Cost"]
optimal_demand = df_results.loc[max_profit_idx, "Demand"]
max_profit = df_results.loc[max_profit_idx, "Profit"]

# Tentukan batas low and high guardrail market price 
low_guardrail = low_price_comp
high_guardrail = high_price_comp

# Plot garis vertikal untuk optimal price dan guardrails
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(df_results["Price"], df_results["Profit"],linewidth=2, linestyle='-', color="#493D9E")

# Garis putus-putus
plt.axvline(x=optimal_price, color='g', linestyle='--', linewidth=1)
plt.axvline(x=low_guardrail, color='#FFB200', linestyle='--', linewidth=1)
plt.axvline(x=high_guardrail, color='#FFB200', linestyle='--', linewidth=1)

# Tambahkan marker untuk profit maksimal
plt.scatter(optimal_price, max_profit, color='green', zorder=5)

# Menghilangkan garis luar canvas
for spine in ax.spines.values():
    spine.set_visible(False)
    
ax.spines['bottom'].set_visible(True)
ax.spines['left'].set_visible(True)
ax.spines['bottom'].set_linewidth(1)
ax.spines['left'].set_linewidth(1)

# Penambahan text
ax_text(x=low_price_comp+13, y=50, 
        s=f"Lowest Market \nPrice <${low_price_comp}>", 
        fontfamily='serif', fontsize=10, ha='center', color="black",
        highlight_textprops=[{'fontproperties': bold_font}
                             ]) 

ax_text(x=high_price_comp-13, y=160, 
        s=f"Highest Market \nPrice <${high_price_comp}>", 
        fontfamily='serif', fontsize=10, ha='center', color="black",
        highlight_textprops=[{'fontproperties': bold_font}
                             ]) 

# Garis Panah
arrow_props1 = dict(color='#FFB200', width=2, head_width=2, head_length=5, radius=-0.3)
arrow_props2 = dict(color='#FFB200', width=2, head_width=2, head_length=5, radius=-0.3)
ax_arrow(tail_position=(low_price_comp+10, 20+15), head_position=(low_price_comp, 20), ax=ax, **arrow_props1)
ax_arrow(tail_position=(high_price_comp-10, 180-15), head_position=(high_price_comp, 180), ax=ax, **arrow_props2)

# Penyempurnaan tambahan
plt.text(45.5, 100, f"Lowering Competitor Prices Drives Profit\nGrowth to                " f" at Price \${optimal_price:.2f}",
          fontsize=18, color="black", ha='left')
plt.text(52.3, 100, f"${max_profit:.2f}",
          fontsize=18, color="green", ha='left',weight="bold")
plt.text(45.5, 90, "Profit Optimization Curve Price vs Demand",
          fontsize=12, weight="bold", color="#727D73", ha='left')


plt.xlabel('Unit Price ($)', fontsize=12,ha='left',color="#727D73", weight="bold",x=0.45)
plt.ylabel('Total Profit ($)', fontsize=12,ha='right',color="#727D73", weight="bold",y=0.6)
plt.ylim(0, max_profit * 1.5)
plt.xlim(30)
plt.yticks(np.arange(0, max_profit * 1.5 + 25, 50), fontfamily="serif", fontsize=8, weight="bold")
plt.xticks( fontfamily="serif", fontsize=8, weight="bold")
plt.grid(False)
plt.legend()
plt.tight_layout()

# Tampilkan grafik
plt.show()

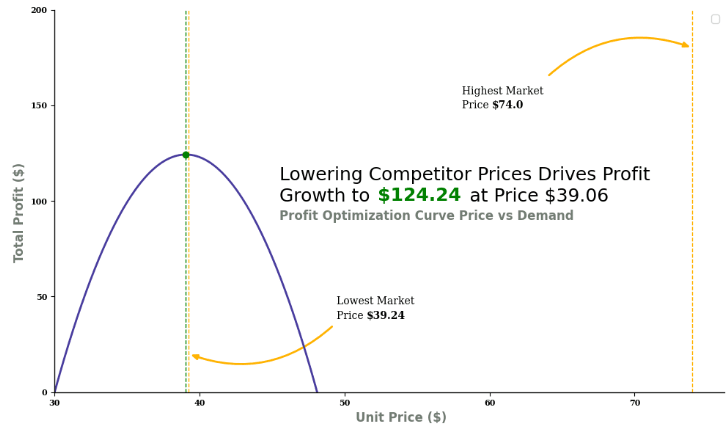
Kurva ini menunjukkan bahwa dengan menetapkan harga sebesar $39.05, yang lebih rendah dari harga pasar terendah sebesar $39.24 (selisih $0.19), kita dapat memperkirakan profit sebesar $124.24. Ini mengindikasikan bahwa penurunan harga masih memberikan keuntungan bagi kita. Namun, perlu diperhatikan bahwa profit dipengaruhi oleh Cost of Goods Sold (COGS), sehingga semakin tinggi COGS, semakin terbatas pula potensi maksimal optimasi profit.

Rekomendasi Bisnis

Dalam customer analytics, Demand Curve merupakan salah satu metrik yang berguna untuk memperkirakan permintaan berdasarkan data historis. Dengan memahami kurva ini, Anda dapat memaksimalkan profit dengan memprediksi jumlah permintaan pada berbagai tingkat harga. Namun, sebelum menerapkan perubahan harga secara luas, disarankan untuk melakukan eksperimen harga pada kelompok sampel terlebih dahulu, mengingat perubahan harga bersifat sensitif bagi konsumen.

Selain itu, penting untuk mengetahui nilai Cost of Goods Sold (COGS) sebelum mengoptimalkan profit. Jika harga jual yang ditetapkan lebih rendah dari COGS, peningkatan jumlah pembelian justru akan memperbesar kerugian. Oleh karena itu, strategi harga harus disusun dengan mempertimbangkan keseimbangan antara permintaan, harga, dan biaya produksi.

Referensi

• Brett Jordan - Unsplash.com

• Wayne L. Winston - Marketing Analytics: Data-Driven Techniques with Microsoft Excel - Books.google.co.id/

• Sean Ellis, Morgan Brown - Hacking Growth: How Today's Fastest-Growing Companies Drive Breakout Success -Books.google.co.id/

• Dawn Fotopulos - Accounting for the Numberphobic: A Survival Guide for Small Business Owners - Books.google.co.id/