Saat berhadapan dengan setumpuk data, pertanyaan pertama yang sering muncul adalah, “Di mana titik pusat data ini?”. Mengetahui nilai “tipikal” atau “rata-rata” adalah langkah fundamental dalam analisis data. Namun, “rata-rata” bisa berarti banyak hal. Apakah itu nilai tengah? Nilai yang paling sering muncul? Atau hasil penjumlahan yang dibagi rata?
Inilah mengapa kita memerlukan ukuran pemusatan data atau tendency central. Ukuran ini adalah sebuah nilai tunggal yang mencoba mendeskripsikan titik pusat dari sekumpulan data.
Dalam panduan ini, kita tidak hanya akan membahas 3 ukuran utama (Mean, Median, Modus), tetapi juga 2 ukuran posisi terkait (Kuartil dan Persentil) yang akan memberikan Anda pemahaman yang lebih kaya tentang distribusi data.
Untuk seluruh contoh, kita akan menggunakan satu set data dummy yang konsisten, yaitu Nilai Kepuasan Pengguna dari 20 partisipan.
| Partisipan | Nilai Kepuasan |
|---|---|
| 0 | 72 |
| 1 | 13 |
| 2 | 67 |
| 3 | 11 |
| 4 | 71 |
| 5 | 18 |
| 6 | 43 |
| 7 | 32 |
| 8 | 60 |
| 9 | 87 |
| 10 | 51 |
| 11 | 13 |
| 12 | 80 |
| 13 | 61 |
| 14 | 49 |
| 15 | 66 |
| 16 | 86 |
| 17 | 78 |
| 18 | 49 |
| 19 | 49 |
Langkah pertama dan terpenting dalam banyak perhitungan statistik adalah mengurutkan data dari yang terkecil hingga terbesar.
Data Terurut:
11, 13, 13, 18, 32, 43, 49, 49, 49, 51, 60, 61, 66, 67, 71, 72, 78, 80, 86, 87
Mari kita mulai bedah satu per satu.
Bagian 1: Ukuran Pemusatan Data (Measures of Central Tendency)
Ini adalah tiga pilar utama untuk menemukan pusat data Anda.
1. Mean (Rata-rata Aritmetika)
Mean adalah ukuran yang paling umum dikenal. Ini adalah jumlah dari semua nilai dibagi dengan banyaknya nilai. Mean sangat baik digunakan ketika data Anda tidak memiliki nilai ekstrem (outlier) yang signifikan.
$$n = 20$$
$$Mean (\bar{x}) = \frac{\sum x_i}{n}$$
$$Mean (\bar{x}) = \frac{11+13+13+...+86+87}{20}$$
$$Mean (\bar{x}) = \frac{1156}{20}$$
$$Mean (\bar{x}) = 57.8$$
R Code
# Vektor data yang sudah diurutkan untuk konsistensi
nilai_kepuasan <- c(11, 13, 13, 18, 32, 43, 49, 49, 49, 51, 60, 61, 66, 67, 71, 72, 78, 80, 86, 87)
mean_nilai <- mean(nilai_kepuasan)
print(paste("Mean dari data tersebut sebesar:", mean_nilai))
Mean dari data tersebut sebesar: 57.8
2. Median (Nilai Tengah)
Median adalah nilai yang berada tepat di tengah kumpulan data yang telah diurutkan. Median adalah pilihan yang jauh lebih baik daripada Mean ketika data Anda memiliki outlier, karena nilainya tidak terpengaruh oleh angka ekstrem.
Karena jumlah data kita genap (n=20), median adalah rata-rata dari dua nilai tengah, yaitu data ke-10 dan data ke-11.
Data ke-10 ($x_{10}$) = 51
Data ke-11 ($x_{11}$) = 60
$$Median (Me) = \frac{x_{10} + x_{11}}{2}$$
$$Median (Me) = \frac{51 + 60}{2}$$
$$Median (Me) = 55.5$$
R Code
median_nilai <- median(nilai_kepuasan)
print(paste("Median dari data tersebut sebesar:", median_nilai))
# Output: "Median dari data tersebut sebesar: 55.5"
3. Modus (Nilai Paling Sering Muncul)
print(paste(“Modus dari data tersebut sebesar:”, paste(modus_hasil$modus, collapse=", “),
“dengan frekuensi:”, modus_hasil$frekuensi))
Output: “Modus dari data tersebut sebesar: 49 dengan frekuensi: 3”
Bagian 2: Memahami Sebaran Data dengan Ukuran Posisi
Terkadang, mengetahui pusat saja tidak cukup. Kita juga perlu tahu bagaimana data tersebar. Di sinilah Kuartil dan Persentil berperan.
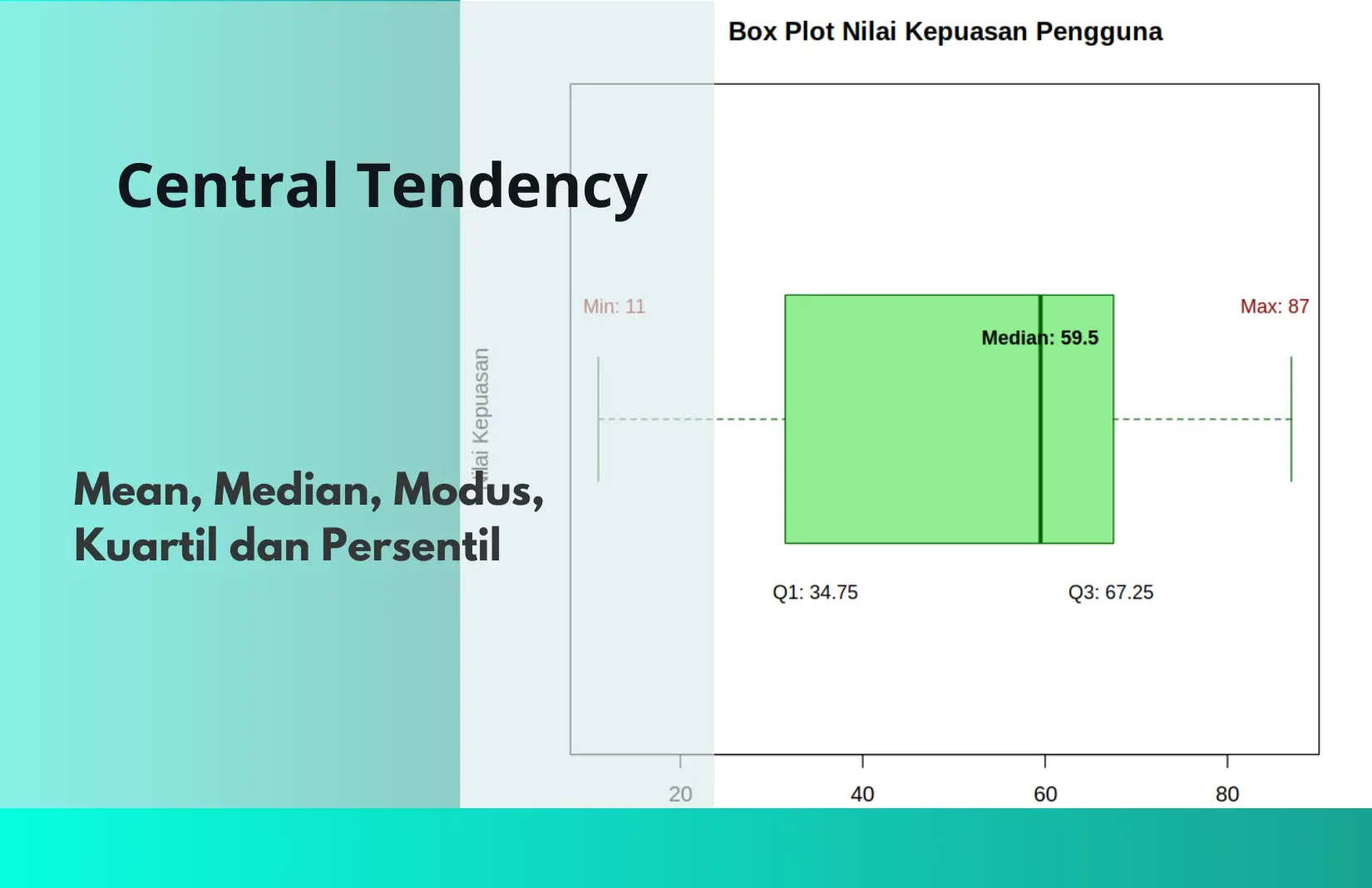
4. Kuartil
Kuartil membagi data yang terurut menjadi empat bagian yang sama besar.
Q1 (Kuartil Bawah) ≈ 34.75
Q2 (Median) = 55.5
Q3 (Kuartil Atas) ≈ 71.75
R Code
summary_stats <- summary(nilai_kepuasan)
print(summary_stats)
# Output:
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 11.00 41.75 55.50 57.80 71.25 87.00
Catatan: Nilai kuartil dari R bisa sedikit berbeda karena metode kalkulasi default (
type=7).
Visualisasi kuartil dengan Box Plot:
boxplot(nilai_kepuasan,
main = "Box Plot Sebaran Nilai Kepuasan",
ylab = "Nilai",
col = "skyblue",
border = "blue",
horizontal = TRUE)
/revisi_boxplot.webp)
5. Persentil
Persentil membagi data menjadi 100 bagian.
Contoh: Persentil ke-90 ($_{90}$).
- $$P_{90} \approx 85.4$$
R Code
persentil <- quantile(nilai_kepuasan, probs = c(0.10, 0.90))
print(persentil)
# Output:
# 10% 90%
# 15.0 81.4
Kesimpulan
Memahami ukuran pemusatan dan posisi adalah dasar dari literasi data. Berikut kapan menggunakannya:
- Gunakan Mean saat data simetris tanpa outlier.
- Gunakan Median saat data memiliki outlier atau condong (skewed).
- Gunakan Modus untuk data kategorikal atau nilai yang paling populer.
- Gunakan Kuartil & Persentil untuk memahami sebaran dan posisi relatif data.
Dengan memilih ukuran yang tepat, Anda akan menarik kesimpulan yang lebih akurat dan tidak mudah terkecoh oleh angka.
Reference :
- Johnson, R. R., & Kuby, P. J. (2004). Elementary statistics (9th ed.). Brooks/Cole.