Statistik Regresi Linear Sederhana dengan R

Misalnya, kita penasaran mengenai hubungan antara kualitas suatu produk dengan tingkat kepuasan pengguna. Asumsinya adalah semakin tinggi kualitas produk yang dirasakan pengguna, maka tingkat kepuasan mereka juga akan semakin tinggi. Dengan kata lain, kita menduga bahwa ada hubungan positif antara persepsi kualitas produk dan kepuasan pelanggan. Untuk menguji asumsi ini secara lebih objektif dan terukur, kita bisa menggunakan metode regresi linear untuk melihat apakah benar terdapat pola hubungan antara kedua variabel tersebut. Atau bisa jadi, persepsi kepuasan tidak hanya dipengaruhi oleh kualitas, melainkan juga faktor lain seperti layanan purna jual atau harga?

Tentu saja, untuk dapat mengukur tingkat kepuasan penggunaan produk, kita memerlukan indikator penilaian yang jelas dan sistematis. Misalnya, kita bisa menilai berbagai aspek produk seperti kekuatan dan daya tahan, fungsionalitas, desain dan estetika, kesesuaian spesifikasi, serta kemudahan penggunaan, yang masing-masing diberi skor dalam rentang 1 hingga 10. Walaupun persepsi kepuasan bersifat subjektif, penilaian ini sebaiknya disusun berdasarkan standar umum atau survei yang telah teruji validitas dan reliabilitasnya.

Beberapa indikator yang bisa digunakan antara lain kepuasan terhadap produk, kepuasan terhadap harga, pengalaman pembelian, pelayanan pelanggan, dan loyalitas pelanggan. Jika kita memiliki 5 indikator penilaian, maka skor maksimum yang dapat dicapai adalah 50, yang menunjukkan tingkat kepuasan yang sangat tinggi. Sebaliknya, nilai yang rendah mengindikasikan adanya ketidakpuasan pengguna terhadap berbagai aspek produk. Sistem penilaian seperti ini penting agar analisis terhadap kepuasan pelanggan dapat dilakukan secara konsisten, objektif, dan berbasis data.

Data

Untuk pemahaman yang lebih dalam, kita akan menggunakan data survey ilustrasi yang dapat diakses 📥 di sini.

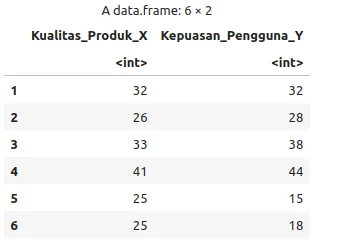
data <- read.csv("data_kepuasan_pelanggan.csv")
head(data)

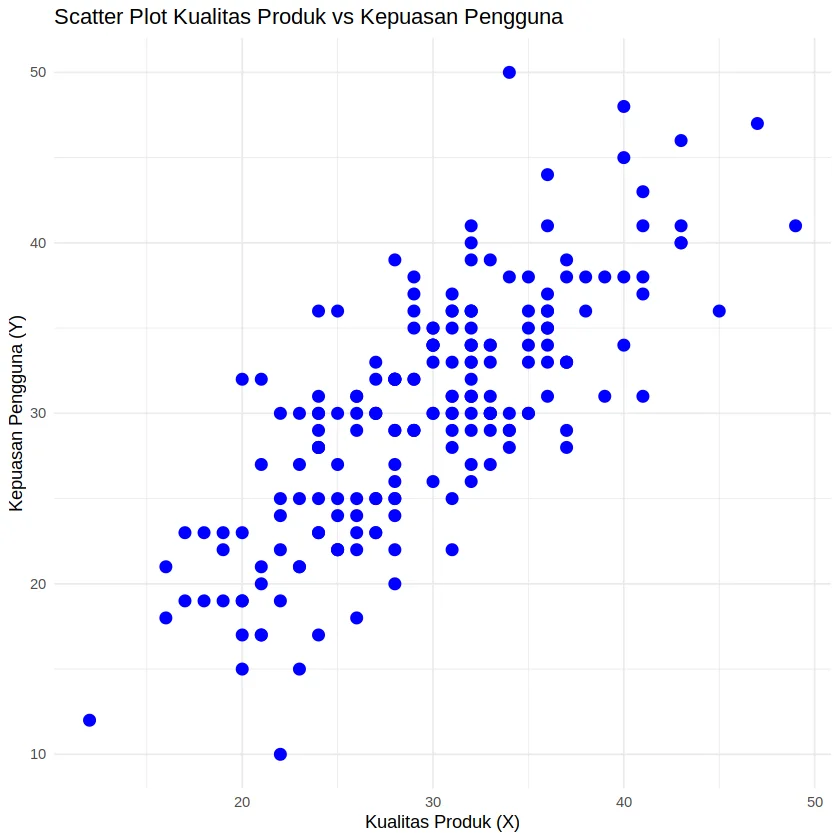
Jika kita melihat hubungannya dengan scatter plot kita dapat melihat hasilnya dengan

library(ggplot2)

# Buat scatter plot
ggplot(data, aes(x = Kualitas_Produk_X, y = Kepuasan_Pengguna_Y)) +
  geom_point(color = "blue", size = 3) +
  labs(title = "Scatter Plot Kualitas Produk vs Kepuasan Pengguna",
       x = "Kualitas Produk (X)",
       y = "Kepuasan Pengguna (Y)") +
  theme_minimal()

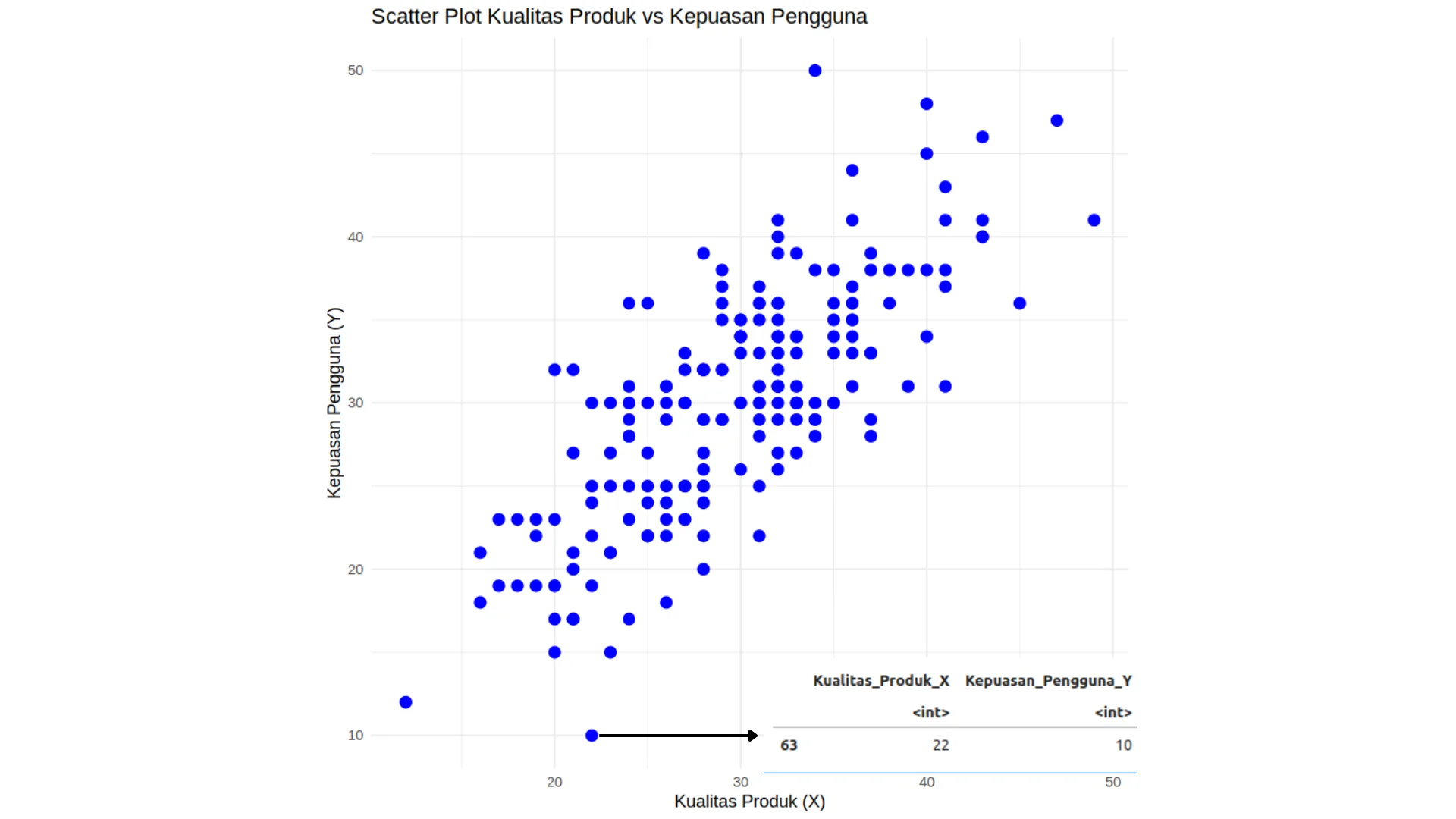
Sebagai informasi, nilai dari titik pada grafik ini merepresentasikan hubungan antara Kualitas Produk dan Kepuasan Pengguna. Misalnya, pada contoh di bawah ini, titik yang ditandai menunjukkan nilai Kualitas Produk sebesar 22 dan nilai Kepuasan Pengguna sebesar 10.

Dari bentuk gambar ini, sebenarnya kita dapat menganalisis apakah hubungan tersebut bersifat positif, negatif, atau tidak memiliki hubungan sama sekali. Gambar ini diambil dari buku Elementary Statistics edisi ke-9, pada pembahasan mengenai Scatter Diagrams and Correlation.

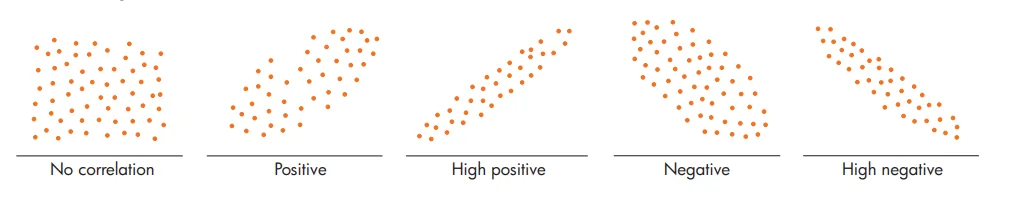
Dari hubungan ini, kita dapat berasumsi bahwa hubungan antara kedua variabel berada pada kategori positif atau positif tinggi (high positive). Artinya, terdapat hubungan positif antara kualitas produk dan kepuasan pelanggan: semakin tinggi kualitas produk, maka semakin tinggi pula tingkat kepuasan pelanggan. Namun, karena kesimpulan ini masih bersifat asumtif, maka diperlukan pengujian statistik untuk menguji validitas hubungan tersebut secara objektif.

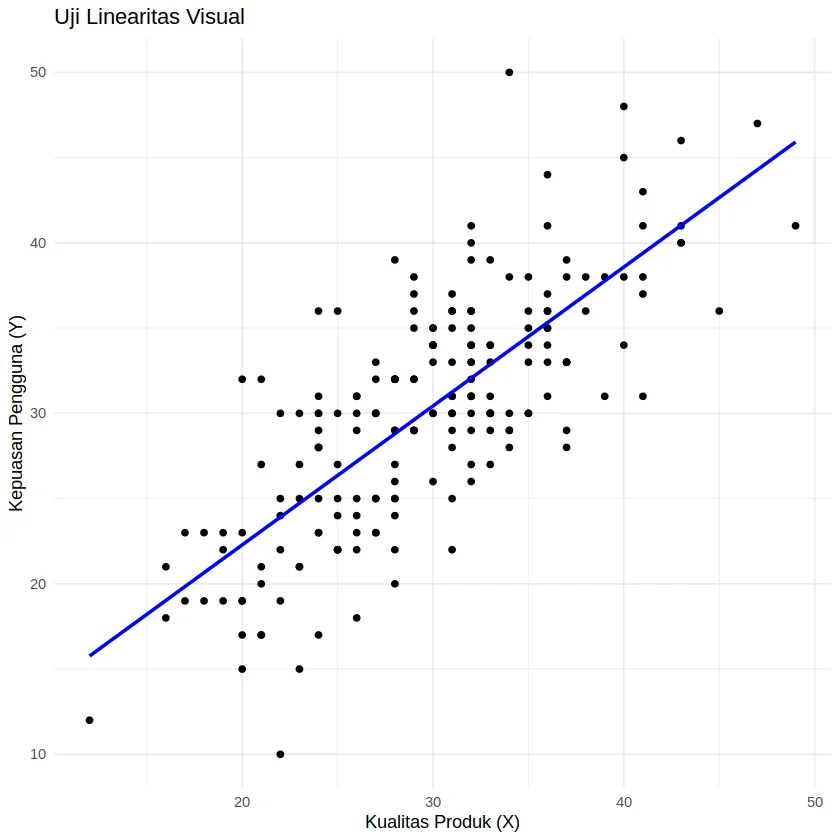
Uji Asumsi 1: Uji Linearitas

Memastikan bahwa hubungan antara variabel independen (X) dan variabel dependen (Y) bersifat linear merupakan asumsi paling fundamental dalam regresi linear sederhana. Asumsi ini memungkinkan kita untuk menilai apakah hubungan antara kedua variabel tersebut cocok dengan model linear (berbentuk garis lurus), atau justru menunjukkan pola yang bersifat non-linear (seperti melengkung, berbentuk kurva, polinomial, atau pola lainnya).

library(ggplot2)

ggplot(data, aes(x = Kualitas_Produk_X, y = Kepuasan_Pengguna_Y)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, color = "blue") +
  labs(title = "Uji Linearitas Visual",
       x = "Kualitas Produk (X)",
       y = "Kepuasan Pengguna (Y)") +
  theme_minimal()

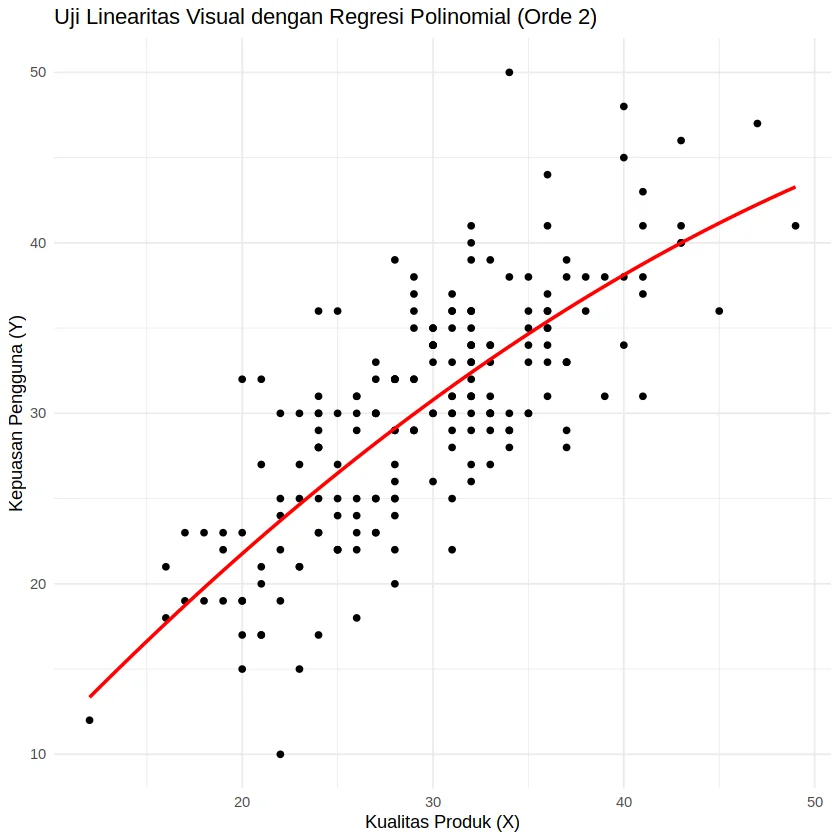
library(ggplot2)

ggplot(data, aes(x = Kualitas_Produk_X, y = Kepuasan_Pengguna_Y)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ poly(x, 2), se = FALSE, color = "red") +
  labs(title = "Uji Linearitas Visual dengan Regresi Polinomial (Orde 2)",
       x = "Kualitas Produk (X)",
       y = "Kepuasan Pengguna (Y)") +
  theme_minimal()

Pemahaman mengenai linearitas sebenarnya cukup sederhana. Kita bisa mengibaratkan garis regresi sebagai jaring ikan. Ketika kita “melempar” jaring ini—baik dalam bentuk garis lurus (regresi linear) maupun lengkung (regresi polinomial atau non-linear)—tujuan utamanya adalah menangkap sebanyak mungkin “ikan”, yaitu titik-titik data.

Nah, pertanyaannya: dengan pola lemparan seperti apa kita bisa menangkap lebih banyak ikan? Di sinilah pentingnya uji linearitas. Jika lemparan dengan garis lurus tidak mampu menangkap banyak titik data (dengan kata lain, tidak lolos uji linearitas), maka kita perlu mengganti pendekatan dengan menggunakan model non-linear. Sederhana, bukan?

Integrasi

model_linear <- lm(Kepuasan_Pengguna_Y ~ Kualitas_Produk_X, data = data)

# Model kuadratik (non-linear)
model_quad <- lm(Kepuasan_Pengguna_Y ~ poly(Kualitas_Produk_X, 2), data = data)

# Bandingkan dengan ANOVA
anova(model_linear, model_quad)

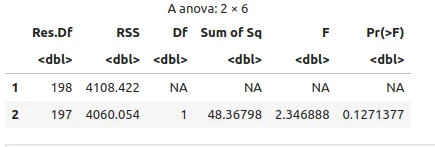
Kesimpulan:

Nilai p (Pr(>F)) = 0.1271 (lebih besar dari 0.05). Ini berarti tidak ada perbedaan signifikan antara model linear dan polynomial. berdasarkan hasil ANOVA ini, model linear (model_linear) dianggap lebih parsimonious (lebih sederhana namun cukup baik) dan lebih disukai daripada model kuadratik (model_quad) untuk data ini.

Untuk perhitungan secara manual dapat dilihat di sini

Uji Asumsi 2: Uji Normalitas Kolmogorov-Smirnov

# Ambil data variabel Y dan X
y <- data$Kepuasan_Pengguna_Y
x <- data$Kualitas_Produk_X

# Hitung rata-rata dan standar deviasi
mean_y <- mean(y)
sd_y <- sd(y)
mean_x <- mean(x)
sd_x <- sd(x)

# Uji Kolmogorov-Smirnov untuk X terhadap distribusi normal
ks_x <- suppressWarnings(
  ks.test(x, "pnorm", mean = mean_x, sd = sd_x)
)

# Uji Kolmogorov-Smirnov untuk Y terhadap distribusi normal
ks_y <- suppressWarnings(
  ks.test(y, "pnorm", mean = mean_y, sd = sd_y)
)

# Tampilkan hasil uji
cat("Hasil Uji K-S untuk X:\n")
print(ks_x)

cat("\nHasil Uji K-S untuk Y:\n")
print(ks_y)

Uji Asumsi 3: Uji Homoskedastisitas

Memastikan bahwa varians dari residual adalah konstan (sama) untuk semua tingkat nilai variabel independen (X). Lawan dari homoskedastisitas adalah heteroskedastisitas (varians residual tidak konstan).

Uji Breusch-Pagan

Interpretasi:

• p-value < 0.05 → terjadi heteroskedastisitas (varians residual tidak konstan).

• p-value ≥ 0.05 → tidak ada bukti heteroskedastisitas (data homoskedastik).

# Install dan panggil package jika belum
if (!require(lmtest)) install.packages("lmtest")
library(lmtest)

# Buat model regresi
model <- lm(Kepuasan_Pengguna_Y ~ Kualitas_Produk_X, data = data)

# Lakukan uji Breusch-Pagan
suppressWarnings(bptest(model))

Kesimpulan:

• P-value = 0.6733

berdasarkan uji Breusch-Pagan dengan tingkat signifikansi 5%, tidak ada bukti statistik yang cukup untuk menyatakan bahwa terdapat masalah heteroskedastisitas dalam model regresi. Dengan kata lain, kita dapat mengasumsikan bahwa asumsi homoskedastisitas (varians error yang konstan) terpenuhi untuk model ini.

Menentukan Korelasi dan Prediksi

Korelasi

Tahapan

• Substitusi Nilai N, $\sum X$, $\sum Y$,$\sum XY$, $\sum X^2$, dan $\sum Y^2$
• $N(\sum X​Y​)−(\sum X​)(\sum Y​)$
• $N(\sum X^2)−(\sum X​)^2$
• $N(\sum Y^2)−(\sum Y)^2$
• Mencari nilai r

Substitusi Nilai N, $\sum X$, $\sum Y$,$\sum XY$, $\sum X^2$, dan $\sum Y^2$

data_r <- data

# Tambahkan kolom XY dan X^2
data_r$XY <- data_r$Kualitas_Produk_X * data_extended$Kepuasan_Pengguna_Y
data_r$X2 <- data_r$Kualitas_Produk_X^2
data_r$Y2 <- data_r$Kepuasan_Pengguna_Y^2

# Lihat hasilnya
head(data_r)

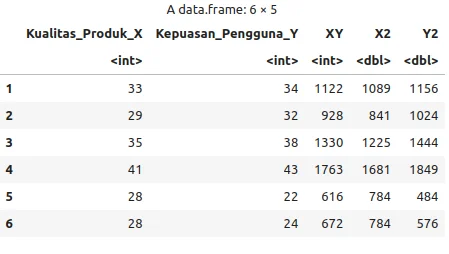
sum_X   <- sum(data_r$Kualitas_Produk_X)
sum_Y   <- sum(data_r$Kepuasan_Pengguna_Y)
sum_XY  <- sum(data_r$XY)
sum_X2  <- sum(data_r$X2)
sum_Y2  <- sum(data_r$Y2)
n <- nrow(data_extended)

# Tampilkan hasilnya
cat("Jumlah X     :", sum_X, "\n")
cat("Jumlah Y     :", sum_Y, "\n")
cat("Jumlah X*Y   :", sum_XY, "\n")
cat("Jumlah X^2   :", sum_X2, "\n")
cat("Jumlah Y^2   :", sum_Y2, "\n")
cat("Jumlah Baris Data   :", n, "\n")

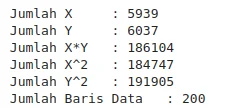
$\sum X$ = 5939; $\sum Y$ = 6037; $\sum XY$ = 186104; $\sum X^2$ = 184747; $\sum Y^2$ = 191905; N (Jumlah baris data) = 200

Pembilang ($N(\sum X​Y​)−(\sum X​)(\sum Y​)$)

# Jumlah data (N)
n <- nrow(data_extended)

# Hitung pembilang dari beta_1
pembilang <- (n * sum_XY) - (sum_X * sum_Y)

# Tampilkan hasil
cat("Pembilang (N * ΣXY - ΣX * ΣY):", pembilang, "\n")

Pembilang (N * ΣXY - ΣX * ΣY): 1367057

Penyebut X($N(\sum X^2)−(\sum X​)^2$)

# Hitung penyebut dari beta_1
penyebut_x <- (n * sum_X2) - (sum_X^2)

# Tampilkan hasil
cat("Penyebut (N * ΣX² - (ΣX)²):", penyebut, "\n")

Penyebut (N * ΣX² - (ΣX)²): 1677679

Pernyebut Y ($N(\sum Y^2)−(\sum Y)^2$)

# Hitung ekspresi
penyebut_y <- n * sum_Y2 - (sum_Y)^2

# Tampilkan hasil
cat("Hasil dari N * ΣY² - (ΣY)² :", penyebut_y, "\n")

Hasil dari N * ΣY² - (ΣY)² : 1935631

Mencari nilai r

Secara sederhana karena kita dapat menyederhanakan melalui perhitungan sebelumnya dengan :

# Hitung r
r <- pembilang / sqrt(penyebut_x * penyebut_y)

# Tampilkan hasil
cat("Koefisien Korelasi (r):", r, "\n")

Koefisien Korelasi (r): 0.7586141

Dari perhitungan tersebut dapat

Integrasi Langsung Untuk Korelasi

• p-value < 0.05 → Ada korelasi yang signifikan.

• p-value ≥ 0.05 → Tidak ada korelasi yang signifikan.

• Koefisien korelasi (r) berada di antara -1 dan 1:

  • r > 0: korelasi positif

  • r < 0: korelasi negatif

  • r = 0: tidak ada korelasi linear

# Uji korelasi Pearson
result <- cor.test(data$Kualitas_Produk_X, data$Kepuasan_Pengguna_Y, method = "pearson")

# Format output yang lebih rapi
cat(sprintf("Hasil Uji Korelasi Pearson:\n"))
cat(sprintf("Koefisien Korelasi (r): %.4f\n", result$estimate))
cat(sprintf("p-value: %.4f\n", result$p.value))

# Interpretasi hasil
if (result$p.value < 0.05) {
  cat("Kesimpulan: Ada korelasi yang signifikan.\n")
} else {
  cat("Kesimpulan: Tidak ada korelasi yang signifikan.\n")
}

Prediksi

Pada dasarnya, estimasi Y dalam model regresi linear adalah hasil dari persamaan regresi, yaitu:

di mana:

• Y adalah nilai yang ingin diprediksi.

• β₀ (Intercept) adalah nilai konstanta (y-intercept) pada model regresi.

• β₁ (Slope) adalah koefisien regresi yang menunjukkan perubahan rata-rata pada Y untuk setiap perubahan satu unit pada X.

• X adalah variabel bebas atau prediktor.

Tahap

• Mencari nilai $\sum X$, $\sum Y$,$\sum XY$, dan $\sum X^2$
• Rata-rata X ($\bar{X}$) dan Rata-rata Y ($\bar{Y}$)
• Menghitung Estimasi Slope ($\beta_{1}$)
• Menghitung Estimasi Slope ($\beta_{0}$)
• Persamaan Regresi Estimasi

Mencari nilai $\sum X$, $\sum Y$,$\sum XY$, dan $\sum X^2$

Pertama kita perlu menghitung nilai untuk kolom baru yaitu $X \times Y$ dan $X^2$

data_extended <- data

# Tambahkan kolom XY dan X^2
data_extended$XY <- data_extended$Kualitas_Produk_X * data_extended$Kepuasan_Pengguna_Y
data_extended$X2 <- data_extended$Kualitas_Produk_X^2

# Lihat hasilnya
head(data_extended)

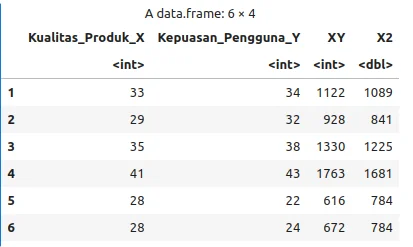
Kemudian,

sum_X   <- sum(data_extended$Kualitas_Produk_X)
sum_Y   <- sum(data_extended$Kepuasan_Pengguna_Y)
sum_XY  <- sum(data_extended$XY)
sum_X2  <- sum(data_extended$X2)

n <-

# Tampilkan hasilnya
cat("Jumlah X     :", sum_X, "\n")
cat("Jumlah Y     :", sum_Y, "\n")
cat("Jumlah X*Y   :", sum_XY, "\n")
cat("Jumlah X^2   :", sum_X2, "\n")

$\sum X$ = 5939; $\sum Y$ = 6037; $\sum XY$ = 186104; dan $\sum X^2$ = 184747 N (Jumlah baris data) = 200

nrow(data_extended)

200

Rata-rata X ($\bar{X}$) dan Rata-rata Y ($\bar{Y}$)

# Jumlah data (jumlah baris)
n <- nrow(data_extended)

# Hitung rata-rata X dan Y menggunakan jumlah yang sudah ada
mean_X <- sum_X / n
mean_Y <- sum_Y / n

# Tampilkan hasilnya
cat("Rata-rata X (Kualitas Produk) : ", mean_X, "\n")
cat("Rata-rata Y (Kepuasan Pengguna) : ", mean_Y, "\n")

Menghitung Estimasi Slope ($\beta_{1}$)

# Hitung koefisien beta_1 menggunakan rumus yang diberikan
beta_1 <- (n * sum_XY - sum_X * sum_Y) / (n * sum_X2 - sum_X^2)

# Tampilkan hasilnya
cat("Koefisien Beta_1 (Slope):", beta_1, "\n")

Menghitung Estimasi Slope ($\beta_{0}$)

Persamaan Regresi Estimasi

Integrasi langsung Prediksi

# Membuat model regresi linear
model <- lm(Kepuasan_Pengguna_Y ~ Kualitas_Produk_X, data = data)
# Mengambil nilai koefisien dari model
intercept <- coef(model)[1]
slope <- coef(model)[2]

# Tampilkan koefisien
cat("Intercept (β₀):", intercept, "\n")
cat("Slope (β₁):", slope, "\n")

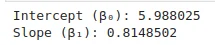
Artinya, model regresi yang diperoleh adalah:

Sama bukan dengan perhitungan manual sebelumnya. Sekarang kita dapat membuat prediksi dengan model tersebut. Misalnya, jika nilai kualitas produk kita dalam skala 50 adalah 30, maka kepuasan pelanggan yang diprediksi dapat dihitung sebagai berikut:

Jadi, dengan nilai kualitas sebesar 30, kepuasan pelanggan yang diprediksi adalah sekitar 30,43. Namun, karena terdapat ketidakpastian dalam setiap prediksi, kita memerlukan interval kepercayaan, yaitu rentang nilai di sekitar prediksi yang mencerminkan tingkat keyakinan kita terhadap hasil tersebut. Umumnya, digunakan interval kepercayaan 95%, yang berarti kita 95% yakin bahwa nilai sebenarnya berada dalam rentang tersebut.

Confidence Interval

Jika nilai kualitas produk sebesar 30, maka nilai kepuasan pengguna yang diprediksi adalah sekitar 30,43.

Namun, karena setiap prediksi mengandung ketidakpastian, kita menggunakan interval kepercayaan 95% untuk memberikan gambaran tentang rentang kemungkinan nilai rata-rata kepuasan sebenarnya.

Tahap :

• Menghitung Nilai Prediksi($\hat Y$)
• Menghitung Standar Error (sₑ)
• Menghitung $S_{XX}$​ dan Rata-rata $X( \bar{X})$
• Menghitung Confidence Interval untuk Prediksi

Menghitung Nilai Prediksi($\hat Y$)

# Misalnya X = 30
X_new <- 30

# Menghitung prediksi Y (ŷ)
Y_pred <- intercept + slope * X_new
cat("Prediksi Y untuk X = 30 adalah:", Y_pred, "\n")

Prediksi Y untuk X = 30 adalah: 30.43353

Menghitung Standar Error (sₑ)

Se adalah kolom jarak perbedaan nilai prediksi dengan nilai sebenarnya. Kita dapat membuat kolom baru dengan

# Menghitung residuals (Y - Y_pred)
residuals <- model$residuals

data$residuals <- residuals
head(data)

# Menghitung standar error (sₑ)
se <- sqrt(sum(residuals^2) / (length(data$Kualitas_Produk_X) - 2))
cat("Standar error (sₑ):", se, "\n")

Standar error (sₑ): 4.555174

Menghitung $S_{XX}$​

Membuat kolom $(X-\bar X)^2$

data_CI <- data
X_bar <- mean(data_CI$Kualitas_Produk_X)

# Menghitung S_{XX} = Σ(Xi - X̄)²
data_CI$dev_kuadrat <- (data_CI$Kualitas_Produk_X - X_bar)^2

# Tampilkan dataset dengan kolom S_XX baru
head(data_CI)

S_XX <- sum(data_CI$dev_kuadrat)
cat("S_XX:", S_XX, "\n")

S_XX: 8388.395

Menghitung Confidence Interval untuk Prediksi

Karena kita memiliki 2 variabel sehingga derajat kebebasan (df) dapat dihitung dengan N - 2(jumlah variabel). Untuk nilai T sendiri dapat dilihat di t tabel (t tabel), tetapi kita juga dapat melakukannya di R

# Jumlah data (N)
N <- nrow(data)

# Derajat kebebasan (N - 2)
df <- N - 2

# Nilai t-kritis untuk tingkat kepercayaan 95%
t_value <- qt(0.975, df)
cat("t_value:", t_value, "\n")

t_value: 1.972017

dengan menyatukan semua nilai yang ada sehingga kita dapat mencari nilai $CI(\bar Y)$ dari nilai X = 30 dengan

# Menghitung interval kepercayaan untuk prediksi Y
CI_lower <- Y_pred - t_value * se * sqrt(1/N + (X_new - X_bar)^2 / S_XX)
CI_upper <- Y_pred + t_value * se * sqrt(1/N + (X_new - X_bar)^2 / S_XX)

cat("Confidence Interval untuk prediksi Y:", CI_lower, "sampai", CI_upper, "\n")

Confidence Interval untuk prediksi Y: 29.79764 sampai 31.06942

Integrasi langsung Confidence Interval

# Buat data baru untuk prediksi saat kualitas produk = 30
data_baru <- data.frame(Kualitas_Produk_X = 30)

# Prediksi dengan interval kepercayaan 95%
prediksi_conf <- predict(model, newdata = data_baru, interval = "confidence", level = 0.95)

# Tampilkan hasil prediksi dan interval kepercayaan
cat("\nPrediksi Kepuasan dengan Interval Kepercayaan 95%:\n")
print(prediksi_conf)

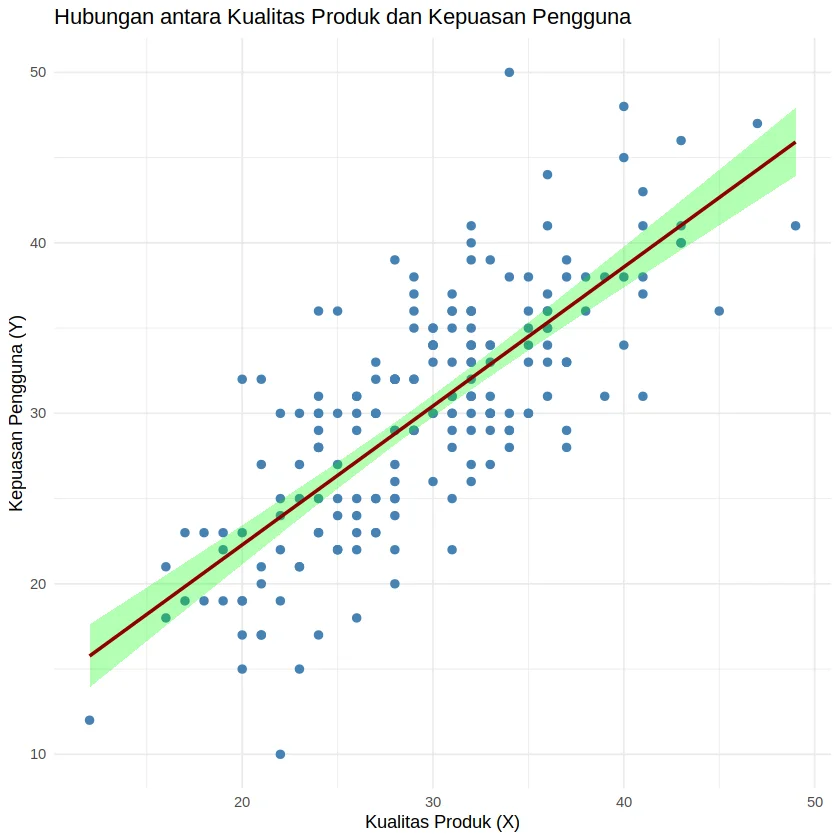
Dengan demikian, kita dapat mengatakan:

Dengan tingkat kepercayaan 95%, kepuasan pengguna rata-rata diperkirakan berada dalam rentang 29,80 hingga 31,07 ketika kualitas produk bernilai 30.

# Pastikan pustaka ggplot2 tersedia
if (!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)

# Plot regresi dengan confidence interval 95%
ggplot(data, aes(x = Kualitas_Produk_X, y = Kepuasan_Pengguna_Y)) +
  geom_point(color = "steelblue", size = 2) +  
  geom_smooth(method = "lm", level = 0.95, color = "darkred", fill = "green", alpha = 0.3) + 
  labs(
    title = "Hubungan antara Kualitas Produk dan Kepuasan Pengguna",
    x = "Kualitas Produk (X)",
    y = "Kepuasan Pengguna (Y)"
  ) +
  theme_minimal()

• Johnson, R. R., & Kuby, P. J. (2004). Elementary statistics (9th ed.). Brooks/Cole.